
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
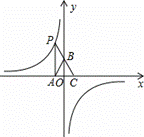 如图,点P是反比例函数
如图,点P是反比例函数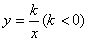 图象上的点,PA垂直
图象上的点,PA垂直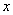 轴于点A(-1,0),点C的坐标为(1,0),PC交
轴于点A(-1,0),点C的坐标为(1,0),PC交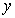 轴于点B,连结AB,已知AB=
轴于点B,连结AB,已知AB=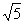
(1)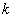 的值是__________;
的值是__________;
(2)若M( ,
, )是该反比例函数图象上的点,且满足
)是该反比例函数图象上的点,且满足
∠MBA<∠ABC,则 的取值范围是__________
的取值范围是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
设边长为4的正方形的对角线长为a,下列关于a的四种说法: a是无理数;‚ a可以用数轴上的一个点来表示;ƒ 4<a<5; „ a是32的算术平方根。其中,所有正确说法的序号是 ( )
A. „ B. ‚ƒ C. ‚„ D. ƒ„
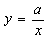 | |||
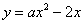 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到,如下是一个案例,请补充完整。
原题:如图1,在⊙O中,MN是直径,AB⊥MN于点B,CD⊥MN于点D,∠AOC=90°,AB=3,CD=4,则BD= 。
⑴尝试探究:如图2,在⊙O中,MN是直径,AB⊥MN于点B,CD⊥MN于点D,点E在MN上,∠AEC=90°,AB=3,BD=8,BE:DE=1:3,则CD= (试写出解答过程)。
⑵类比延伸:利用图3,再探究,当A、C两点分别在直径MN两侧,且AB≠CD,AB⊥MN于点B,CD⊥MN于点D,∠AOC=90°时,则线段AB、CD、BD满足的数量关系为 。
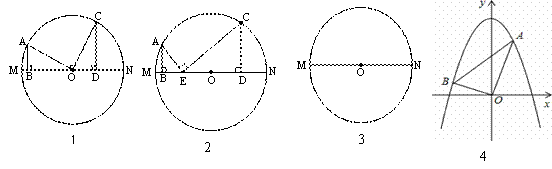 ⑶拓展迁移:如图4,在平面直角坐标系中,抛物线经过A(m,6),B(n,1)两点(其中0<m<3),且以y轴为对称轴,且∠AOB=90°,①求mn的值;②求抛物线的解析式。
⑶拓展迁移:如图4,在平面直角坐标系中,抛物线经过A(m,6),B(n,1)两点(其中0<m<3),且以y轴为对称轴,且∠AOB=90°,①求mn的值;②求抛物线的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线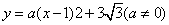 经过点
经过点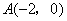 ,抛物线的顶点为
,抛物线的顶点为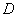 ,过
,过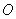 作射线
作射线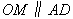 .过顶点
.过顶点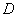 平行于
平行于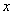 轴的直线交射线
轴的直线交射线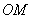 于点
于点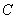 ,
,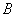 在
在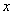 轴正半轴上,连结
轴正半轴上,连结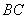 .
.
(1)求该抛物线的解析式;
(2)若动点 从点
从点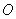 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线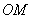 运动,设点
运动,设点 运动的时间为
运动的时间为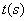 .问当
.问当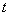 为何值时,四边形
为何值时,四边形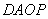 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?
(3)若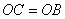 ,动点
,动点 和动点
和动点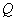 分别从点
分别从点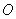 和点
和点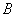 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿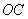 和
和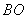 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为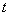
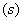 ,连接
,连接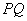 ,当
,当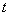 为何值时,四边形
为何值时,四边形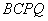 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时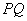 的长.
的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
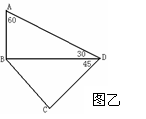
用一副三角板拼出甲、乙两个图形,
求:图甲中,,∠CFD, ∠AEF的度数。
图乙中,用尺规(用直尺、圆规作图,并保留作图痕迹
作出BD的中点E。点E与点A、C的距离相等吗?请说明理由。
 |  | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com