
【题目】如图,在菱形ABCD中,∠BAD=84°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
A.64°
B.54°
C.60°
D.84°
【答案】B
【解析】解:连接BD,BF,
∵∠BAD=84°,
∴∠ADC=96°,
又∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠FAD=∠FDA=42°,
∴∠CDF=96°﹣42°=54°.
故选B.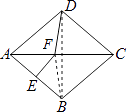
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】按要求作图
(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知△ABC中,∠C是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求∠ABC与∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
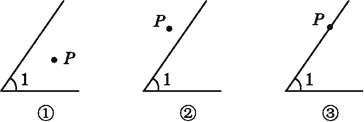
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示某市2016年6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
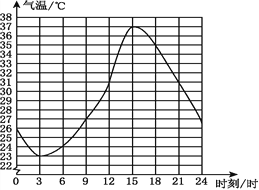
(1)这天的最高气温是多少摄氏度?
(2)这天共有多少个小时的气温在31 ℃以上?
(3)这天什么时间范围内气温在上升?
(4)请你预测一下,次日凌晨1时的气温大约是多少摄氏度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
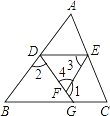
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=________.(________.),
∴AB∥EF(________.)
∴∠3=________.(________.)
又∠B=∠3(已知)
∴∠B=________.(等量代换)
∴DE∥BC(________.)
∴∠C=∠AED(________.).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com