
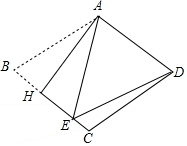
 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
分析 根据翻折变换的性质可得AB=AE,然后根据等腰三角形两底角相等求出∠B=∠AEB=70°,根据菱形的四条边都相等可得AB=AD,菱形的对角相等求出∠ADC,再求出∠DAE,然后根据等腰三角形两底角相等求出∠ADE,然后根据∠EDC=∠ADC-∠ADE计算即可得解.
解答 解:∵菱形ABCD沿AH折叠,B落在BC边上的点E处,
∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB=$\frac{1}{2}$(180°-40°)=70°,
在菱形ABCD中,AB=AD,∠ADC=∠B=70°,
AD∥BC,
∴∠DAE=∠AEB=70°,
∵AB=AE,AB=AD,
∴AE=AD,
∴∠ADE=$\frac{1}{2}$(180°-∠DAE)=$\frac{1}{2}$(180°-70°)=55°,
∴∠EDC=∠ADC-∠ADE=70°-55°=15°.
故选B.
点评 本题考查了翻折变换的性质,菱形的性质,等腰三角形两底角相等的性质,翻折前后对应边相等,菱形的四条边都相等,对角相等.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
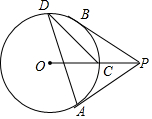 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )| A. | 26° | B. | 20° | C. | 16° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com