
| a2+1 |
| b2+4 |
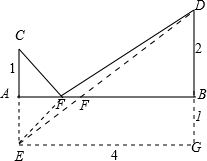 解:作图如下所示,作AC⊥AB,BD⊥AB,
解:作图如下所示,作AC⊥AB,BD⊥AB,| a2+1 |
| b2+4 |
| (4-a)2+4 |
| a2+1 |
| b2+4 |
| a2+1 |
| b2+4 |
| 32+42 |
| a2+1 |
| b2+4 |


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
| x+y-8 |
| 8-x-y |
| 3x-y-a |
| x-2y+a+3 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省黄冈市浠水县望城实验中学九年级(上)第一次月考数学试卷(解析版) 题型:解答题
 ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:《第21章 二次根式》2009年复习(解析版) 题型:解答题
 ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《二次根式》(05)(解析版) 题型:解答题
 ,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、a的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com