
 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.分析 由直角三角形斜边上的中线性质得出OA=$\frac{1}{2}$BC=OB=OC,由等腰三角形的性质得出OE⊥AB,AE=BE,AD=CD,OD⊥AC,证出四边形ADOE为矩形,得出AE=OD,AD=OE,求出OD=AE=$\frac{1}{2}$AB=4,OE=AD=$\frac{1}{2}$AC=3,即可得出四边形ADOE的周长.
解答 解:∵∠BAC=90°,O为BC的中点,
∴OA=$\frac{1}{2}$BC=OB=OC,
∵OE平分∠AOB,OD平分∠AOC,
∴OE⊥AB,AE=BE,AD=CD,OD⊥AC,
∴∠AEO=∠ADO=90°,
∴四边形ADOE为矩形,
∴AE=OD,AD=OE,
∵AB=8,AC=6,
∴OD=AE=$\frac{1}{2}$AB=4,OE=AD=$\frac{1}{2}$AC=3,
∴四边形ADOE的周长=2(AD+AE)=2(3+4)=14.
点评 本题考查了矩形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的性质;熟练掌握矩形的判定与性质,由等腰三角形的三线合一性质得出OE⊥AB,AE=BE,AD=CD,OD⊥AC是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
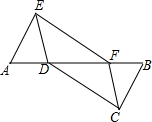 如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.
如图,在△AEF中,点D,B分别在边AF和AF的延长线上,已知FB=AD,BC∥AE,且BC=AE,连结CD,CF,DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
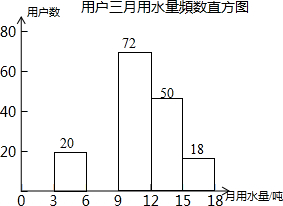 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
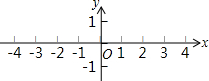 如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.
如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,1),C(-4,0).画出△ABC,并画出△ABC关于y轴对称的图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com