
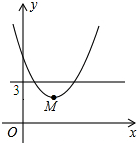
 在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.
在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2. 分析 分三种情况:点M的纵坐标小于2;点M的纵坐标等于2;点M的纵坐标大于2;进行讨论即可得到方程$\frac{1}{5}$x2+bx+c=2的解的个数.
解答 解:分三种情况:
点M的纵坐标小于2,方程$\frac{1}{5}$x2+bx+c=2的解是2个不相等的实数根;
点M的纵坐标等于2,方程$\frac{1}{5}$x2+bx+c=2的解是2个相等的实数根;
点M的纵坐标大于2,方程$\frac{1}{5}$x2+bx+c=2的解的个数是0.
故方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.
故答案为:0,1或2.
点评 考查了抛物线与x轴的交点,二次函数的性质,本题涉及分类思想和方程思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
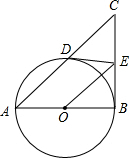 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
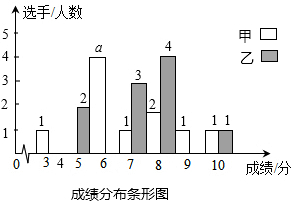 某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:
某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:| 成绩/队别 | 平均分 | 中位数 | 方差 | 合格率% | 优秀率% |
| 甲队 | 6.9 | m | 3.41 | 9 | n |
| 乙队 | 6.8 | x-1 | 3.25 | 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个等边三角形一定全等 | B. | 腰对应相等的两个等腰三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 全等三角形的面积一定相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com