
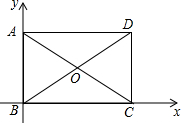
 矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.
矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4.分析 (1)易知AB=CD=OA=OB=OC=OD=4,在Rt△BCD中求出BC即可;
(2)分两种情形求解①如图2中,当EF⊥AD时,易知AE=DE=4,此时E(4,4).②如图3中,当EF⊥BD时,分别求解即可;
解答 解:(1)如图1中,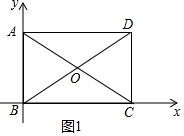
∵四边形ABCD是矩形,
∴OA=OC=OD=OB,
∴△ABO是等边三角形,
∴AB=CD=OD=OC=4,
∴BD=8,
在Rt△BCD中,BC=$\sqrt{B{D}^{2}-D{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴D(4$\sqrt{3}$,4),
故答案为(4$\sqrt{3}$,4).
(2)①如图2中,当EF⊥AD时,易知AE=DE=4,此时E(4,4).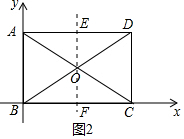
②如图3中,当EF⊥BD时,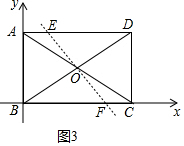
在Rt△EOD中,cos∠EDO=$\frac{OD}{DE}$=$\frac{AD}{BD}$,
∴$\frac{4}{DE}$=$\frac{4\sqrt{3}}{8}$,
∴DE=$\frac{8\sqrt{3}}{3}$,
∴AE=8-$\frac{8\sqrt{3}}{3}$,
∴E(8-$\frac{8\sqrt{3}}{3}$,4),
综上所述,满足条件的点E坐标为(4,4)或(8-$\frac{8\sqrt{3}}{3}$,4).
点评 本题考查坐标与图形的性质、矩形的性质,直角三角形的判定,锐角三角函数等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
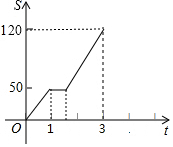 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com