
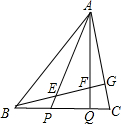
 如图,BP:PQ:QC=1:2:1,CG:AG=1:2,则BE:EF:FG=
如图,BP:PQ:QC=1:2:1,CG:AG=1:2,则BE:EF:FG=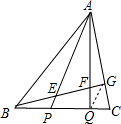 解:连接GQ,由题干的比例关系可得GQ∥AP,
解:连接GQ,由题干的比例关系可得GQ∥AP,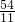 .
.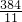 ,S△AFG=18-x=18-
,S△AFG=18-x=18-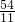 =
=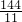 ,
,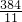 :
: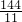 =11:16:6.
=11:16:6.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:
| BP | CQ |
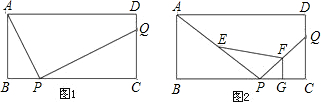 的中点,求四边形EPGF的面积.
的中点,求四边形EPGF的面积.查看答案和解析>>
科目:初中数学 来源:第19章《相似形》中考题集(17):19.6 相似三角形的性质(解析版) 题型:解答题
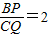 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.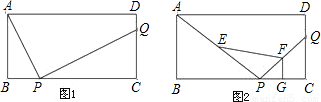
查看答案和解析>>
科目:初中数学 来源:第24章《相似形》中考题集(22):24.3 相似三角形的性质(解析版) 题型:解答题
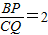 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.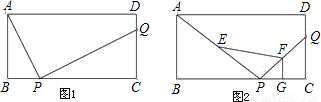
查看答案和解析>>
科目:初中数学 来源:2011年广东省深圳市中考数学模拟试卷(05)(解析版) 题型:解答题
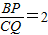 ,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.
,且E,F,G分别为AP,PQ,PC的中点,求四边形EPGF的面积.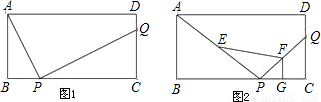
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com