D
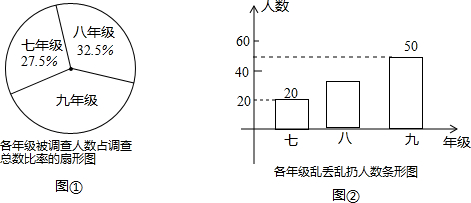
分析:由2000乘以20%求出调查学生的总数,进而求出七、八、九年级的学生总数,由七、九年级乱扔垃圾的人数求出各自乱扔垃圾的比率,减去七、九年级乱扔垃圾的人数求出八年级乱扔垃圾的人数,求出八年级乱扔垃圾的比率,根据条形统计图求出乱丢垃圾的比率,即可作出判断.
解答:根据题意得:2000×20%=400(人),
∴七年级调查的学生数为400×27.5%=110(人);八年级调查的学生数为400×32.5%=130(人);九年级调查的学生数为400-110-130=160(人),
∴九年级实际人数为160÷20%=800(人);
根据条形统计图得到七年级乱丢乱扔的比率为
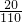
=
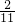
;
∵七、八、九年级乱扔垃圾的总人数为400×25%=100(人),
∴八年级乱扔垃圾的人数为100-(20+50)=30(人),
∵八年级乱丢垃圾的比率为

≈23%<25%;九年级乱丢乱扔的比率为
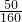
=

,
则七年级乱丢乱扔的比率最低;八年级乱丢乱扔的比率低于25%;九年级实际人数为800人,即正确的有①②③.
故选D
点评:此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.

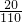 =
=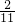 ;
; ≈23%<25%;九年级乱丢乱扔的比率为
≈23%<25%;九年级乱丢乱扔的比率为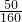 =
= ,
,

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案