
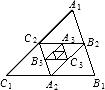
 如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是
如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |


科目:初中数学 来源: 题型:
 如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn=
如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于( )
如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于( )| A、12 | B、13 | C、14 | D、15 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=( )
如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
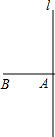 如图,已知直线l,点A在I上,线段AB=1cm,且AB⊥l.我们规定:把线段AB先沿直线l翻折得到A1′B1′(即线段AB与线段A1′B1′关于l成轴对称),再沿射线A1′B1′方向平移1cm得到线段A1B1,称为第一次变换;再将线段A1B1先沿直线l翻折得到A2′B2′,再沿射线A2′B2′方向平移1cm得到线段A2B2.称为第二次变换.
如图,已知直线l,点A在I上,线段AB=1cm,且AB⊥l.我们规定:把线段AB先沿直线l翻折得到A1′B1′(即线段AB与线段A1′B1′关于l成轴对称),再沿射线A1′B1′方向平移1cm得到线段A1B1,称为第一次变换;再将线段A1B1先沿直线l翻折得到A2′B2′,再沿射线A2′B2′方向平移1cm得到线段A2B2.称为第二次变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com