解:(1)△BEC可以由△ABD绕点B顺时针旋转60°得到.
理由如下:
∵△ABE,△BCD都是等边三角形,
∴BA=BE,BD=BC,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
∴△ABD绕点B顺时针旋转60°可得到△BEC;
(2)AD=EC.理由如下:
∵△ABE,△BCD都是等边三角形,
∴BA=BE,BD=BC,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC 中,
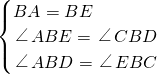
,
∴△ABD≌△EBC,
∴AD=EC;
②锐角∠CFD的度数不改变.理由如下:
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠FCD+∠FDC=∠FCD+∠BDC+∠ADB
=∠BCE+∠FCD+∠BDC
=∠BCD+∠BDC
=60°+60°
=120°
∴∠CFD=180°-(∠FCD+∠FDC)=180°-120°=60°.
分析:(1)根据等边三角形的性质得到BA=BE,BD=BC,∠ABE=∠CBD=60°,则∠ABD=∠EBC,根据旋转的定义得到△ABD绕点B顺时针旋转60°可得到△BEC;
(2)根据等边三角形的性质得到BA=BE,BD=BC,∠ABE=∠CBD=60°,则∠ABD=∠EBC,易证得△ABD≌△EBC,根据全等的旋转即可得到AD=EC;
(3)由△ABD≌△EBC得到∠BCE=∠BDA,则有∠FCD+∠FDC=∠FCD+∠BDC+∠ADB=∠BCE+∠FCD+∠BDC=∠BCD+∠BDC=60°+60°=120°,根据三角形内角和定理即可得到∠CFD的度数.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,并且它们的夹角也相等的两三角形全等;全等三角形的对应边相等、对应角相等.也考查了等边三角形的性质.


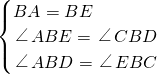 ,
,

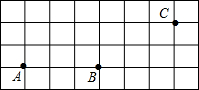 如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等.
如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等. 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中: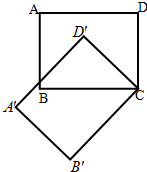 25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题: