
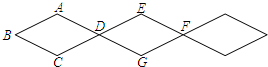
 如图是利用四边形的不稳定性制作的菱形凉衣架.已知其中每个菱形的边长为13cm,
如图是利用四边形的不稳定性制作的菱形凉衣架.已知其中每个菱形的边长为13cm,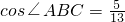 ,那么凉衣架两顶点A、E之间的距离为________cm.
,那么凉衣架两顶点A、E之间的距离为________cm. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
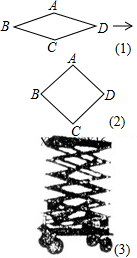 (2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.| 2 |
查看答案和解析>>
科目:初中数学 来源:辽宁省朝阳市2011年初中毕业升学考试数学试卷 题型:044
如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.

(1)如图是一个基本图形,已知AB=1米,当∠ABC为30°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);

(2)当∠ABC从30°变为90°(如图是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.
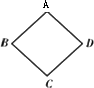
[结果精确到0.1米,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,![]() ≈1.41]
≈1.41]
查看答案和解析>>
科目:初中数学 来源:辽宁省中考真题 题型:解答题

 ≈1.41]
≈1.41] 查看答案和解析>>
科目:初中数学 来源:2013年湖北省随州市曾都区实验中学中考数学模拟试卷(一)(解析版) 题型:解答题
 ≈1.41].
≈1.41].
查看答案和解析>>
科目:初中数学 来源:2011年辽宁省朝阳市中考数学试卷(解析版) 题型:解答题
 ≈1.41].
≈1.41].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com