科目：初中数学 来源： 题型：
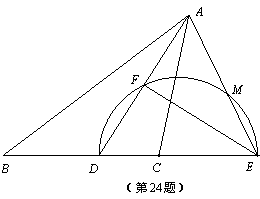
已知，在△ABC中，AD为∠BAC的平分线，点E在BC的延长线上，且∠EAC＝∠B，以DE为直径的半圆交AD于点F，交AE于点M．
（1）判断AF与DF的数量关系，并说明理由；
（2）只用无刻度的直尺画出△ADE的边DE上的高AH；
（3）若EF＝4，DF＝3，求DH的长．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
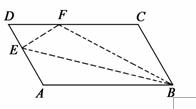
如图，平行四边形ABCD中，点E在边AD上，以BE为折痕，将△ABE折叠，使点A正好与CD上的F点重合，若△FDE的周长为16，△FCB的周长为28，则FC的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
某学习小组想了解南京市“迎青奥”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．
（1）在上述调查方式中，你认为最合理的是 (填序号)；
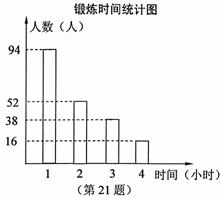
（2）由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图，请直接写出这200名居民健身时间的众数、中位数；
 |
（3）小明在求这200名居民每人健身时间的平均数时，他是这样分析的：
 |
小明的分析正确吗？如果不正确，请求出正确的平均数；
（4）若我市有800万人，估计我市每天锻炼2小时及以上的人数是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
在一次聚餐中，小明发现用圆形铁盘加热食物时，铁盘边缘部分的食物先熟，中间部分的食物后熟，说明铁盘不同位置的温度有差异．针对这一现象，他收集了如下统计图表：
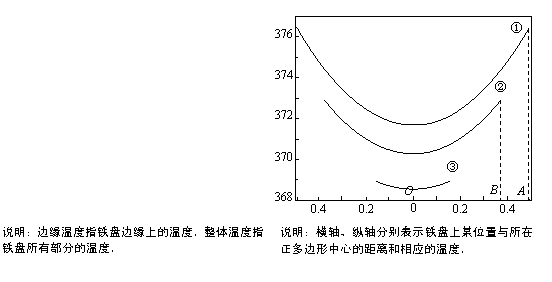
表一 正多边形铁盘温度方差表 图一 正多边形铁盘温度分布统计图（部分）
 |
| 正多边形边数 | 边缘温度方差 | 整体温度方差 |
| 4 | 2.30 | 4.73 |
| 6 | 0.34 | 3.05 |
| 8 | 0.10 | 2.60 |
| 10 | 0.05 | 2.52 |
| 12 | 0.02 | 2.51 |
| 无穷多：圆 | 0.00 | 2.30 |
（1）表一中，随着正多边形边数的增加，边缘温度方差如何变化？边缘温度最稳定的是哪一种形状的铁盘？
（2）图一中，最有可能表示圆形铁盘温度分布的曲线序号是 ．
（3）已知各正多边形（包含圆）的面积相等．图一中点A、B的数值对应曲线的端点，点O表示正多边形中心．观察图一，下列说法正确的有 ．（填写正确选项的序号）
a．可以看出，曲线②表示的整体温度比曲线③表示的整体温度稳定．
b．OA与OB长度不同，其意义是不同正多边形的顶点距各自中心的距离不同．
c．曲线②表示的铁盘的边数比曲线①表示的铁盘的边数少．
d．如果曲线①代表正四边形，且OA2︰OB2＝3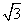
︰4，那么曲线②可以代表正六边形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
交，最多有
个交点，最少有
个交点，则
_____.
＋1) (3-
图，在边长为3 cm的正方形ABCD中，点E为BC边上的任意一点，AF⊥AE，AF交CD的延长线于F，则四边形AFCE的面积为 cm 2.