
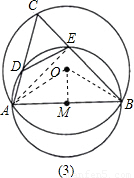
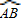 上的一个动点(不与点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
上的一个动点(不与点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2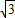 .
.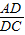 =x(0<x<3),那么在点C的运动过程中,试用含x的代数式表示y.
=x(0<x<3),那么在点C的运动过程中,试用含x的代数式表示y.
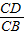 的值,能计算出DE的长.
的值,能计算出DE的长.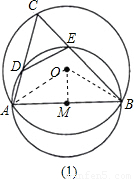 解:(1)如图:连接OB、OM.
解:(1)如图:连接OB、OM.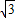 ,∴OM=1.
,∴OM=1.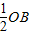 ,∴∠OBM=30°.
,∴∠OBM=30°. ∠AOB=60°.
∠AOB=60°.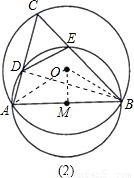
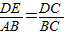 .
.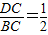 .即
.即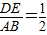 .
.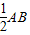 =
= ×2
×2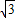 =
=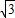 .
.
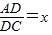 ,可得AD=x•DC,AC=AD+DC=(x+1)•DC.
,可得AD=x•DC,AC=AD+DC=(x+1)•DC. ,sin∠ACE=
,sin∠ACE= ,
,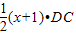 ;
;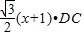 .
.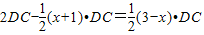 .
.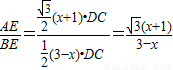 ,
,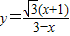 (0<x<3).
(0<x<3).

科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
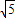 ,sin∠OAB=
,sin∠OAB= .
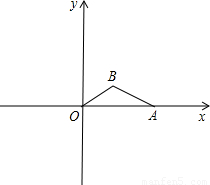
.
查看答案和解析>>
科目:初中数学 来源:2008年四川省成都市中考数学试卷(解析版) 题型:解答题
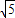 ,sin∠OAB=
,sin∠OAB=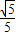 .
.
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《圆》(05)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年河北省廊坊市安次区九年级网络试卷设计大赛数学试卷(3)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com