
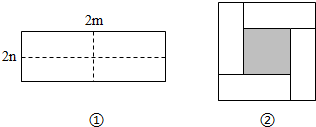
分析 (1)观察图形很容易得出图②中的阴影部分的正方形的边长等于a-b,①求出小正方形的边长,②运用大正方形的面积减去四个矩形的面积.
(2)根据(1)中表示的面积是同一个图形的面积,两个式子相等,即可列出等量关系;
(3)由(2)中的等量关系即可求解.
解答 解:(1)根据图形可观察出:边长为a-b;
①小正方的边长为a-b,面积可表示为:(a-b)2,大正方形的面积为:(a+b)2,四个矩形的面积和为4ab,所以小正方形面积可表示为:(a+b)2-4ab;
故答案为:(a-b)2,(a+b)2-4ab;
(2)能;由分析得:(a-b)2=(a+b)2-4ab;
(3)由(2)很快可求出(a-b)2=(a+b)2-4ab=62-4×8=4.
点评 本题考查了完全平方公式的实际应用,完全平方公式与正方形的面积公式和长方形的面积公式经常联系在一起,要学会观察.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
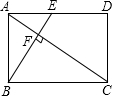 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
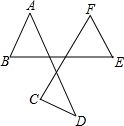 如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
如图,A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图:A、B、C、D四点在同一直线上,若AB=CD.
(1)如图:A、B、C、D四点在同一直线上,若AB=CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
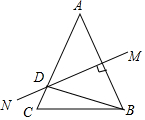 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 45° | C. | 55° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com