
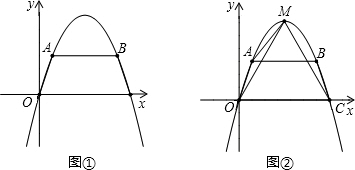
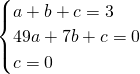 ,
,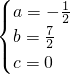 ,
, x2+
x2+ x;
x; ×36+
×36+ ×6=3,
×6=3,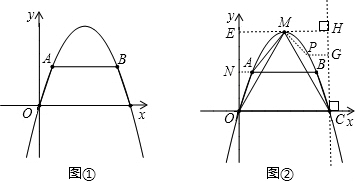
 ,
, )
) m2+
m2+ m.
m. (1+
(1+ )(
)( -3)=
-3)=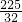 ,△AON的面积=
,△AON的面积= ×1×3=
×1×3= ;
; (7-m+
(7-m+ )[
)[ -(-
-(- m2+
m2+ m)],△PGC的面积等于:
m)],△PGC的面积等于: (7-m)×(-
(7-m)×(- m2+
m2+ m)
m) (7-m+
(7-m+ )[
)[ -(-
-(- m2+
m2+ m)]+
m)]+ (7-m)×(-
(7-m)×(- m2+
m2+ m)=
m)=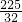 +
+

 ,
,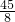 );
);  或m≤-
或m≤- .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
 P,使S四边形POCA=S△AOB?若存在,请直接写出点P的坐标;若不存在,请简要说明理由.
P,使S四边形POCA=S△AOB?若存在,请直接写出点P的坐标;若不存在,请简要说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 四边形OABC是等腰梯形,OA∥BC.在建立如图的平面直角坐标系中,A(4,0),B(3,2),点M从O点以每秒2个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速度向终点C运动,过点N作NP垂直于x轴于P点连接AC交NP于Q,连接MQ.
四边形OABC是等腰梯形,OA∥BC.在建立如图的平面直角坐标系中,A(4,0),B(3,2),点M从O点以每秒2个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速度向终点C运动,过点N作NP垂直于x轴于P点连接AC交NP于Q,连接MQ.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,直线y=6-x与双曲线y=
如图,在直角坐标系中,直线y=6-x与双曲线y=| 4 |
| x |
| A、4,6 | B、4,12 |
| C、8,6 | D、8,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
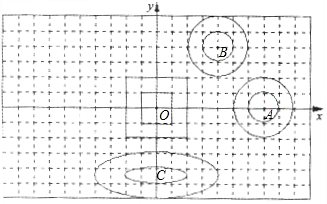 的一个共同特征:
的一个共同特征:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com