
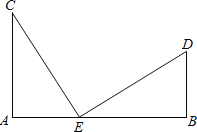
【题目】如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,
(1)△AEC≌△BDE吗,请说明理由
(2)试猜想线段CE与DE大小与位置关系,说明理由.
【答案】见解析
【解析】先利用HL判定△AEC≌△BDE,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:(1)△AEC≌△BDE,理由为:
因为AC⊥AB,DB⊥AB,所以∠CAE=∠DBE=90°,
又因为AC=BE,AE=BD,所以△AEC≌△BDE.
(2)CE=DE,CE⊥DE,理由为:
由(1)可知,△AEC≌△BDE,所以CE=DE,∠C=∠DEB,
又因为在Rt△AEC中,∠C+∠CEA=90°,
所以∠DEB+∠CEA=90°,所以∠CED=90°,
所以CE⊥DE.
“点睛”本题考查了全等三角形的判定和性质,垂直的定义、平角的定义,熟练掌握全等三角形的判定定理是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如下图、表所示:
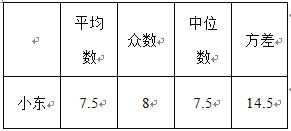
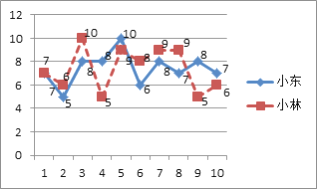
若让你选择其中一名参加比赛则你选择的运动员是:__________________________,
理由是:_____________________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com