
如图,在 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为圆心的半圆分别与
为圆心的半圆分别与 、
、 边相切于
边相切于 、
、 两点,连接
两点,连接 .已知
.已知 ,
, .求:
.求:

(1)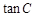 ;
;
(2)图中两部分阴影面积的和.
(1)2/3,(2) 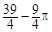
【解析】解:(1)连接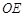
∵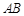 、
、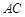 分别切
分别切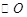 于
于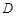 、
、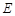 两点
两点
∴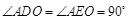
又∵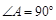
∴四边形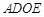 是矩形
是矩形
∵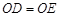
∴四边形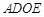 是正方形. .................................(2分)
是正方形. .................................(2分)
∴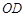 ∥
∥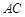 ,
,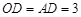
∴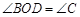
∴在 中,
中,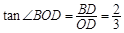
∴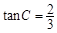 .
.................................(5分)
.
.................................(5分)
(2)如图,设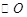 与
与 交于
交于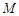 、
、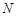 两点.由(1)得,四边形
两点.由(1)得,四边形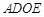 是正方形
是正方形
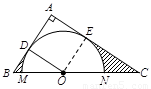
∴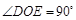
∴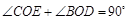
∵在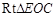 中,
中,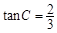 ,
,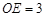
∴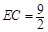 .
.................................(7分)
.
.................................(7分)
∴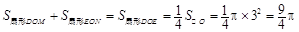
∴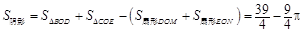
∴图中两部分阴影面积的和为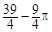 ............ 9分
............ 9分
(1)连接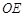 ,求得四边形
,求得四边形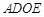 是正方形,得出AD的长,从而求得
是正方形,得出AD的长,从而求得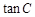
(2)根据阴影面积等于三角形的面积减去扇形的面积求得


科目:初中数学 来源: 题型:
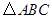 中,
中,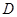 是
是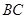 边上的一点,
边上的一点,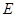 是
是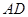 的中点,过点
的中点,过点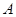 作
作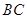 的平行线AF与
的平行线AF与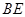 的延长线交于点
的延长线交于点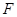 ,且
,且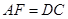 ,连结
,连结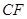 .
.
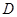 是
是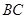 的中
的中 点;
点;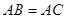 ,试判断四边形
,试判断四边形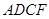 的形状,并证明你的结论.
的形状,并证明你的结论.查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市潮南区中考模拟考试数学卷 题型:解答题
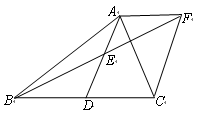
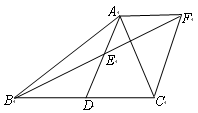
已知:如图,在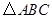 中,
中,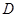 是
是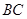 边上的一点,
边上的一点,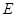 是
是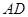 的中点,过点
的中点,过点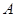 作
作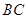 的平行线AF与
的平行线AF与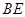 的延长线交于点
的延长线交于点 ,且
,且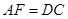 ,连结
,连结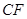 .
.
【小题1】(1)求证: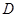 是
是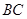 的中
的中 点;
点;
【小题2】(2)如果 ,试判断四边形
,试判断四边形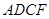 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东临沂青云镇中心中学八年级下学期期末考试数学卷(带解析) 题型:解答题
如图,在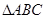 中,
中,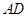 是边
是边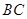 上的中线,过点
上的中线,过点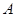 作
作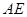 ∥
∥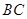 ,过
,过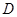 作
作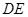 ∥
∥ ,
,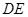 与
与 、
、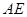 分别交于点
分别交于点 、点
、点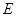 ,连接
,连接 .
.
(1)求证: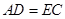 ;
;
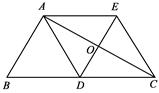
(2)当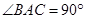 时,求证:四边形
时,求证:四边形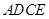 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com