练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    62、要了解一批灯管的使用寿命，从中抽取了20只进行测试，在个问题中，总体是
    一批灯管的使命寿命
    ，样本是
    抽取的20只灯管的使用寿命
    分析：总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．
    解答：解：本题考查的对象是一批灯管的使用寿命，故总体是一批灯管的使命寿命，样本是抽取的20只灯管的使用寿命．
    点评：解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    下列说法中，正确的有（　　）
    ①腰相等的两个等腰三角形全等；
    ②三角之比为3：4：5的三角形是直角三角形；
    ③在△ABC中，AB=AC=x，BC=6，则腰长x的取值范围是3＜x＜6；
    ④要了解一批灯管的使用寿命，从中选取了20只进行测试，在这个问题中20支灯管是样本容量；
    ⑤已知△ABC的三边长分别是a，b，c，且
    a
    b
    +
    a
    c
    =
    b+c
    b+c-a
    ，则△ABC一定是底边长为a的等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列调查，不适合采用抽样方式的是（　　）

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江杭州萧山区党湾镇初中八年级12月月考数学试卷（带解析） 题型：单选题

    下列说法中，正确的有（     ）
    ①腰相等的两个等腰三角形全等；②三角之比为3：4：5的三角形是直角三角形；③在中，AB=AC=x，BC=6，则腰长x的取值范围是3<x<6；④要了解一批灯管的使用寿命，从中选取了20只进行测试，在这个问题中20支灯管是样本容量；⑤已知的三边长分别是a、b、c，且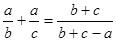，则一定是底边长为a的等腰三角形

    A．0个　　B．1个 　　C．2个 　　D．3个

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江杭州萧山区党湾镇初中八年级12月月考数学试卷（解析版） 题型：选择题

    下列说法中，正确的有（     ）

    ①腰相等的两个等腰三角形全等；②三角之比为3：4：5的三角形是直角三角形；③在中，AB=AC=x，BC=6，则腰长x的取值范围是3<x<6；④要了解一批灯管的使用寿命，从中选取了20只进行测试，在这个问题中20支灯管是样本容量；⑤已知的三边长分别是a、b、c，且，则一定是底边长为a的等腰三角形

    A．0个　　          B．1个 　　         C．2个 　　         D．3个

     

    查看答案和解析>>

    同步练习册答案