写出图象经过点(1,0)、(0,1)的三个不同的函数解析式:________.
y=-x+1,y=

x
2-

x+1,y=-x
2+1
分析:(1)可设函数为一次函数为y=kx+b,将点(1,0)、(0,1)分别代入解析式,求出k、b的值;
(2)设函数为y=ax
2+bx+c,将点(1,0)、(0,1)、(2,0)分别代入解析式,求出a、b、c的值;
(3)设函数为y=ax
2+c,将点(1,0)、(0,1)分别代入解析式,求出a、c的值;
从而可得三个不同的解析式.
解答:(1)设函数为一次函数为y=kx+b,
将点(1,0)、(0,1)分别代入解析式得:
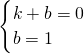
,
解得
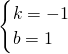
,
函数解析式为y=-x+1;
(2)设函数为y=ax
2+bx+c,
将点(1,0)、(0,1)、(2,0)分别代入解析式得:
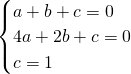
,
解得
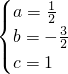
,
函数解析式为y=

x
2-

x+1.
(3)设函数为y=ax
2+c,将点(1,0)、(0,1)分别代入解析式得,
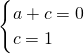
,
解得
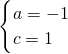
,
函数解析式为y=-x
2+1.
故答案为y=-x+1,y=

x
2-

x+1,y=-x
2+1.
点评:本题考查了待定系数法求函数解析式,要熟悉各种函数的一般表达式,方可解答.

 x2-
x2- x+1,y=-x2+1
x+1,y=-x2+1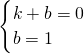 ,
,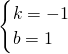 ,
,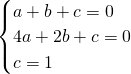 ,
,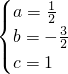 ,
, x2-
x2- x+1.
x+1.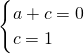 ,
,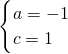 ,
, x2-
x2- x+1,y=-x2+1.
x+1,y=-x2+1.
