
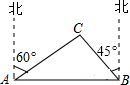
 我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(
我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.( ≈1.732,
≈1.732, ≈1.414)
≈1.414) 解:(1)道路AB不穿过电力设施区域.
解:(1)道路AB不穿过电力设施区域. =
= x(米),
x(米), x+x=2000,
x+x=2000, -1000≈732,
-1000≈732,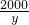 -5=
-5=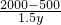 +
+ ,
, x+x=2000,解此方程即可求得CD的长,与700米比较,即可得道路AB不穿过电力设施区域;
x+x=2000,解此方程即可求得CD的长,与700米比较,即可得道路AB不穿过电力设施区域;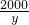 -5=
-5=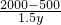 +
+ ,解此分式方程即可求得答案.
,解此分式方程即可求得答案.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
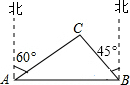 (2011•鄂尔多斯)我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(
(2011•鄂尔多斯)我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011年内蒙古鄂尔多斯市中考数学试卷(解析版) 题型:解答题
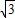 ≈1.732,
≈1.732,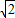 ≈1.414)
≈1.414)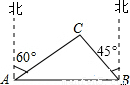
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com