

���� ��1���������������������ռ�İٷֱ������������
��2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����鵽������ѧ��ǡ����һ���ó��鷨����һ���ó��滭������������ø��ʹ�ʽ������ô𰸣�
��� �⣺��1�����꼶��1����ѧ��������Ϊ��12��25%=48���ˣ���
�ʴ�Ϊ��48��
��2���ֱ���A��B��ʾ�����ó��鷨��ѧ������C��D��ʾ�����ó��滭��ѧ����
����״ͼ�ã�
�߹���12�ֵȿ��ܵĽ�����鵽������ѧ��ǡ����һ���ó��鷨����һ���ó��滭����8�������
��鵽������ѧ��ǡ����һ���ó��鷨����һ���ó��滭�ĸ���Ϊ��$\frac{8}{12}$=$\frac{2}{3}$��
���� ���⿼�����б�������״ͼ��������Լ�����ͳ��ͼ������ͳ��ͼ���õ���֪ʶ��Ϊ������=������������������֮�ȣ�


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��6��2��4 | B�� | 4��6��5��10 | C�� | 1��$\sqrt{2}$��$\sqrt{3}$��$\sqrt{6}$ | D�� | 2$\sqrt{5}$��$\sqrt{15}$��4��2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
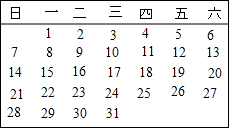 ��ͼ��ij�µ�����������ȡ�������������֣����ǵĺͿ����ǣ�������
��ͼ��ij�µ�����������ȡ�������������֣����ǵĺͿ����ǣ�������| A�� | 18 | B�� | 33 | C�� | 38 | D�� | 75 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
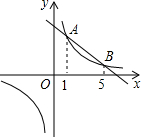 ��ͼ��ֱ��y=k1x+b��k1��0����˫����y=$\frac{{k}_{2}}{x}$��k2��0������A��B���㣬�������ֱ�Ϊ1��5����ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��0��1��x��5��
��ͼ��ֱ��y=k1x+b��k1��0����˫����y=$\frac{{k}_{2}}{x}$��k2��0������A��B���㣬�������ֱ�Ϊ1��5����ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��0��1��x��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5 �� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��-|-3| | B�� | ��-3��2��3 | C�� | -��-25����52 | D�� | -a��|-a| |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com