
 已知抛物线的不等式为y=-x2+6x+c.
已知抛物线的不等式为y=-x2+6x+c.分析 (1)由题意△≥0,列出不等式即可解决问题.
(2)利用根与系数关系,列出方程即可解决问题.
(3)设P(m,n),则Q(n,m),列出方程组,求出m与n的关系,得到关于n的方程,根据判别式大于0,即可解决问题.
解答 解:(1)∵抛物线与x轴有交点,
∴b2-4ac≥0,
∴36+4c≥0,
∴x≥-9.
(2)∵x1+x2=6,x1x2=-c,
∴x12+x22=(x1+x2)2-2x1x2=36+2c=26
∴c=-5.
(3)∵△OPA≌△QOB,
∴OA=BQ,AP=OB,
∴可以设P(m,n),则Q(n,m)
将P(m,n),Q(n,m)代入原解析式中得:$\left\{\begin{array}{l}{-{m}^{2}+6m+c=n}&{①}\\{-{n}^{2}+6n+c=m}&{②}\end{array}\right.$,
①-②得:n2-m2+6m-6n=n-m
∴n2-m2+7m-7n=0,
∴(n-m)(n+m-7)=0,
∴m=n或m=7-n,
∵m,n不相等,
∴m=7-n,
将m=7-n代入①得:n2-7n+7-c=0,
∵b2-4ac>0,
∴49-4(7-c)>0,
c>-$\frac{21}{4}$.
点评 本题考查二次函数综合题、根与系数的关系、方程组等知识,解题的关键是灵活应用所学知识,学会利用参数,构建一元二次方程解决问题,属于中考压轴题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
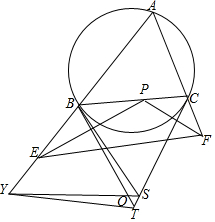 如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.
如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:
观察下列每对数在数轴上的对应点之间的距离:4与-2,3与5,-2与-6,-4与3.并回答下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
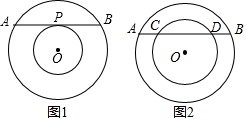
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数3.20和近似数3.2都精确到十分位 | |
| B. | 近似数3.20×103和近似数3.2×103都精确到百位 | |
| C. | 近似数2千万和近似数2000万都精确到千万位 | |
| D. | 近似数32.0和近似数3.2都精确到十分位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com