
解:(1)证明:(方法一)∵AF⊥DE,
∴∠1+∠3=90°即:∠3=90°-∠1,
∴∠2+∠4=90°即:∠4=90°-∠2,
又∵∠1=∠2,
∴∠3=∠4,
∴AE=EF,
∵AD∥BC,
∴∠2=∠5,
∵∠1=∠2,
∴∠1=∠5,
∴AE=AD,
∴EF=AD,
∵AD∥EF,
∴四边形AEFD是平行四边形,
又∵AE=AD,
∴四边形AEFD是菱形,
(方法二)∵AD∥BC,
∴∠2=∠5,
∵∠1=∠2,
∴∠1=∠5,
∵AF⊥DE,
∴∠AOE=∠AOD=90°,
在△AEO和△ADO中

,
∴△AEO≌△ADO,
∴EO=OD
在△AEO和△FEO中

,
∴△AEO≌△FEO,
∴AO=FO,
∴AF与ED互相平分,
∴四边形AEFD是平行四边形,
又∵AF⊥DE,
∴四边形AEFD是菱形;
(2)∵菱形AEFD,
∴AD=EF,
∵BE=EF,
∴AD=BE,
又∵AD∥BC,

∴四边形ABED是平行四边形,
∴AB∥DE,
∴∠BAF=∠EOF,
同理可知四边形AFCD是平行四边形,
∴AF∥DC,
∴∠EDC=∠EOF,
又∵AF⊥ED,
∴∠EOF=∠AOD=90°,
∴∠BAF=∠EDC=∠EOF=90°,
∴∠5+∠6=90°,
∴∠BAD+∠ADC=∠BAF+∠6+∠5+∠EDC=270°;
(3)由(2)知∠BAF=90°平行四边形AFCD,
∴AF=CD=n,
又∵AB=m,

,
由(2)知平行四边形ABED,
∴DE=AB=m,
由(1)知OD=


,
S
四边形ABCD=S
△ABF+S
四边形AFCD=mn.
分析:(1)先证明是平行四边形,再证出一组邻边相等就可以证明菱形.
(2)把要求的角拆成几个角,先分别求出一些角的和,最终求出∠BAD+∠ADC的度数;
(3)把求四边形ABCD的面积转化成求三角形ABF的面积加上平行四边形AFCD的面积,从而求出值.
点评:本题考查了菱形的判定定理,平行线的性质,三角形的面积以及全等三角形的判定和性质定理等.

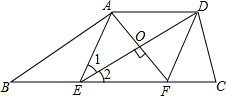 如图,AD∥BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O.
如图,AD∥BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O. 解:(1)证明:(方法一)∵AF⊥DE,
解:(1)证明:(方法一)∵AF⊥DE, ,
, ,
,
 ,
,
 ,
,
