

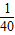 x+
x+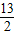 ,最后乘以其销售量x即可得出答案;
,最后乘以其销售量x即可得出答案;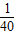 x+
x+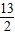 ,
,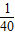 x+
x+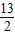 )x=-
)x=-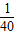 x2+
x2+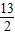 x.
x.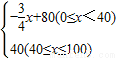
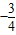 (100-x)+80](100-x)=-
(100-x)+80](100-x)=- x2+70x+500
x2+70x+500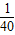 x2+
x2+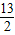 x)+(-
x)+(- x2+70x+500)=-
x2+70x+500)=-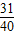 x2+
x2+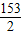 x+500,
x+500,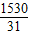 时,w的值最大,
时,w的值最大, x+80)(100-x),
x+80)(100-x), x2-150x+8000,
x2-150x+8000,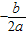 时取得.
时取得. 

 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
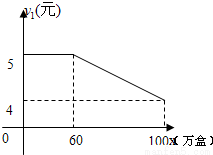
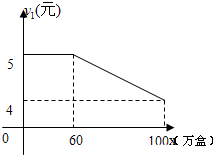 潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=
潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:y2=
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
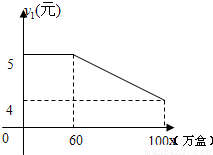
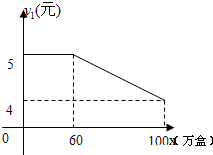 潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:
潍坊市昌乐县有一个食品厂,该厂的食品主要有两种销售方式,一种方式是卖给食品经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的食品都可以全部销售,该食品厂每年可以生产食品100万盒,其中,卖给食品经销商每盒食品的利润y1(元)与销售量x(万盒)之间的函数图如图所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为: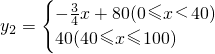
查看答案和解析>>
科目:初中数学 来源:2012-2013学年河北省邢台二中九年级(上)第一次月考数学试卷(解析版) 题型:解答题
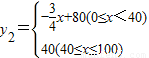

查看答案和解析>>
科目:初中数学 来源:2012年江苏省扬州市宝应县望直港中学中考数学三模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com