Question

15．实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图1，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2．
（1）如图2，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射．若被b反射出的光线n与光线m平行，且∠1=50°，则∠2=100°，∠3=90°．
（2）在（1）中m∥n，若∠1=55°，则∠3=90°；若∠1=40°，则∠3=90°．
（3）由（1）、（2），请你猜想：当两平面镜a、b的夹角∠3=90°时，可以使任何射到平面镜a上的光线m，经过平面镜a、b的两次反射后，入射光线m与反射光线n平行．你能说明理由吗？
（4）如图3，两面镜子的夹角为α°（0＜α＜90）时，进入光线与离开光线的夹角为β°
（0＜β＜90）．试探索α与β的数量关系．直接写出答案．2α+β=180°．

Answer 1

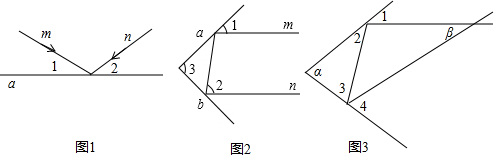
分析 （1）根据平面镜反射光线的规律得∠1=∠4=50°，再利用平角的定义得∠5=80°，然后利用平行线的性质计算出∠2=100°，则∠6=40°，再利用三角形内角和定理计算∠3；
（2）运用同样的方法进行解答即可；
（3）当∠3=90°时，根据三角形内角和定理得∠4+∠6=90°，则2∠4+2∠6=180°，利用平角的定义得到∠2+∠5=180°，然后根据平行线的判定得到m∥n；
（4）由（1）可得，∠5=180°-2∠2，∠6=180°-2∠3，再根据∠2+∠3=180°-∠α，即可得出∠β=180°-∠5-∠6=2（∠2+∠3）-180°=2（180°-∠α）-180°=180°-2∠α．

解答 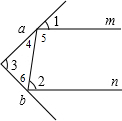解：（1）∵∠1=∠4=50°，
∴∠5=180°-2×50°=80°，
∵m∥n，
∴∠2+∠5=180°，
∴∠2=100°，
∴∠6=$\frac{1}{2}$（180°-∠2）=40°，
∴∠3=180°-∠4-∠6=90°；
故答案为：100°，90°；

（2）同样的方法，可得当∠1=55°，∠3=90°；当∠1=40°，∠3=90°；
故答案为：90°，90°；

（3）当∠3=90°时，m∥n．
理由如下：
∵∠3=90°，
∴∠4+∠6=90°，
∴2∠4+2∠6=180°，
∴∠2+∠5=180°，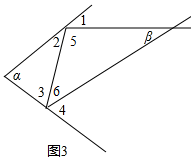
∴m∥n；
故答案为：90°；

（4）①如图3，由（1）可得，∠5=180°-2∠2，∠6=180°-2∠3，
∵∠2+∠3=180°-∠α，
∴∠β=180°-∠5-∠6=2（∠2+∠3）-180°=2（180°-∠α）-180°=180°-2∠α，
∴α与β的数量关系为：2α+β=180°，
故答案为：2α+β=180°．

点评 本题考查了平行线的判定与性质以及三角形内角和定理，解题时注意：同旁内角互补，两直线平行；两直线平行，同旁内角互补．