练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．已知：如图，△ABC．
    求作：直线MN，使MN经过点A，MN∥BC．（尺规作图，保留作图痕迹，不写作法，注意描黑）

    分析 直接利用作一角等于已知角的方法得出MN的位置即可．

    解答 解：如图所示：MN即为所求．

    点评 此题主要考查了复杂作图以及平行线的判定方法，正确掌握作一角等于已知角的方法是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

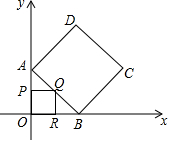    20．如图，在直角坐标系中，已知A（0，4）、B（4，0），以AB为边在第一象限内作正方形ABCD，在三角形AOB内部做正方形OPQR，使P、R、Q三点分别在线段OA、OB、AB上，将正方形OPQR绕点O顺时针旋转时，求点C到点Q距离的最大值与最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

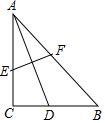    1．如图，在Rt△ABC中，∠C=90°，AC=BC，AD是BC边上的中线，将A点翻折与点D重合，得到折痕EF，则$\frac{CE}{AE}$=$\frac{3}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知△ABC中，AB=5，AC=7，BC=a，则a的取值范围是（　　）
    A．1＜a＜6B．5＜a＜7C．2＜a＜12D．10＜a＜14

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若y=（m-3）xn-1是正比例函数，则m≠3，n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如果规定向东为正，汽车向东行驶3km记作3km，向西行驶2km应记作-2km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

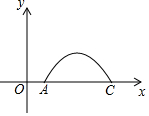    18．如图，一大桥有一段抛物线型的拱粱，小王骑自行车从O匀速沿直线到拱粱一端A，再匀速通过拱粱部分的桥面AC，小王从O到A用了3秒，当小王骑自行车行驶10秒时和20秒时拱粱的高度相同，则小王骑自行车通过拱粱部分的桥面AC共需24秒．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

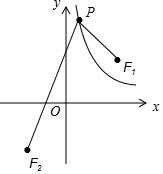    15．已知直线l1：y=-x+$\sqrt{2}$k，双曲线C：y=$\frac{{k}^{2}}{x}$定点F1（$\sqrt{2}$k，$\sqrt{2}$k）．
    （1）若k=$\sqrt{2}$，求直线l1，双曲线C的解析式，定点F的坐标；
    （2）在（1）的条件下，定点F1（$\sqrt{2}$k，$\sqrt{2}$k）关于原点的对称点记作F2，在双曲线C上任取一点P（x，y），求|PF2-PF1|的值；
    （3）若k为大于0的任意实数，定点F1（$\sqrt{2}$k，$\sqrt{2}$k）关于原点的对称点记作F2，在双曲线C上任取一点P（x，y），判断|PF2-PF1|的值是否为定值？若是，求出定值；若不是，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图①，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连接EF．
    （1）说明线段BE与AF的位置关系和数量关系；
    （2）如图②，当△CEF绕点C顺时针旋转α（0°＜α＜90°）时，连接AF，BE，（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，请说明理由；
    （3）如图③，当△CEF绕点C顺时针旋转α（0°＜α＜180°）时，延长FC交AB于点D，如果AD=6-2$\sqrt{3}$，求旋转角α的度数．

    查看答案和解析>>

    同步练习册答案