
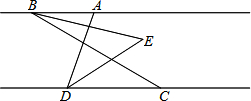
分析 (1)根据角平分线的定义即可求∠EDC的度数;
(2)过点E作EF∥AB,然后根据两直线平行内错角相等,即可求∠BED的度数;
(3)∠BED的度数改变.过点E作EF∥AB,先由角平分线的定义可得:∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,∠CDE=$\frac{1}{2}$∠ADC=35°,然后根据两直线平行内错角相等及同旁内角互补可得:∠BEF=180°-∠ABE=180°-$\frac{1}{2}$n°,∠CDE=∠DEF=35°,进而可求∠BED=∠BEF+∠DEF=180°-$\frac{1}{2}$n°+35°=215°-$\frac{1}{2}$n°.
解答 解:(1)∵DE平分∠ADC,∠ADC=70°,
∴∠EDC=$\frac{1}{2}$∠ADC=$\frac{1}{2}$×70°=35°;
(2)过点E作EF∥AB,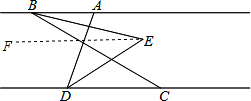
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,∠CDE=$\frac{1}{2}$∠ADC=35°,
∴∠BED=∠BEF+∠DEF=$\frac{1}{2}$n°+35°;
(3)∠BED的度数改变.
过点E作EF∥AB,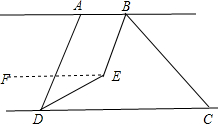
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∴∠ABE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$n°,∠CDE=$\frac{1}{2}$∠ADC=35°
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-$\frac{1}{2}$n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°-$\frac{1}{2}$n°+35°=215°-$\frac{1}{2}$n°.
点评 此题考查了平行线的判定与性质,解题的关键是:正确添加辅助线,及作出(3)中的图形.


科目:初中数学 来源: 题型:选择题
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 3.284×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
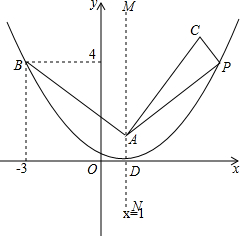 如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.
如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 标号是奇数 | B. | 标号是3 | C. | 标号大于6 | D. | 标号小于6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
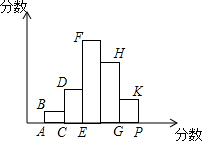 如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.若80分成绩为优秀,则优秀率是38.9%.
如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.若80分成绩为优秀,则优秀率是38.9%.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com