
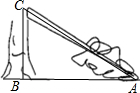
 如图,在一次强台风中,一棵大树在距地面5m的C点处折断倒下,倒下后树顶端着地点A距树底端B的距离为12m,求这棵树原来的高度.
如图,在一次强台风中,一棵大树在距地面5m的C点处折断倒下,倒下后树顶端着地点A距树底端B的距离为12m,求这棵树原来的高度.科目:初中数学 来源: 题型:
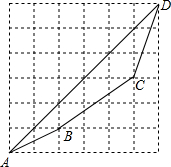 比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较
比较两个实数大小的方法很多,用构造法来比较大小,体现了数形结合的思想,别具一格.例如比较| 5 |
| 10 |
| 13 |
| 2 |
| 5 |
| 13 |
| 10 |
| 2 |
| 5 |
| 10 |
| 13 |
| 2 |
| 10 |
| 2 |
| 61 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com