
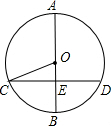
 (2012•珠海)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,那么sin∠OCE=
(2012•珠海)如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,那么sin∠OCE=| 5 |
| 13 |
| 5 |
| 13 |
科目:初中数学 来源: 题型:
 (2012•珠海)如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(2012•珠海)如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•珠海)如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.
(2012•珠海)如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•珠海)如图,水渠边有一棵大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°.求C处到树干DO的距离CO.(结果精确到1米)(参考数据:
(2012•珠海)如图,水渠边有一棵大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°.求C处到树干DO的距离CO.(结果精确到1米)(参考数据:| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•珠海)如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
(2012•珠海)如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•珠海)如图,在等腰梯形ABCD中,AB∥DC,AB=3
(2012•珠海)如图,在等腰梯形ABCD中,AB∥DC,AB=3| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com