
分析 (1)将c=1代入原方程,利用公式法解一元二次方程,即可得出方程的根;
(2)由x12-2x1x2+x22=0可得出x1=x2,结合根的判别式即可得出关于c的一元一次方程,解之即可得出c的值.
解答 解:(1)当c=1时,原方程为x2-4x+1=0,
解得:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{4±\sqrt{(-4)^{2}-4}}{2}$=2±$\sqrt{3}$,
∴x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
(2)∵x12-2x1x2+x22=0,
∴(x1-x2)2=0,
∴x1=x2,
∴△=(-4)2-4c=16-4c=0,
解得:c=4.
∴c的值为4.
点评 本题考查了根的判别式以及公式法解一元二次方程,解题的关键是:(1)熟练掌握公式法解一元二次方程的方法;(2)由x12-2x1x2+x22=0找出16-4c=0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
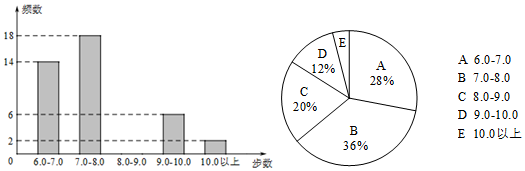
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
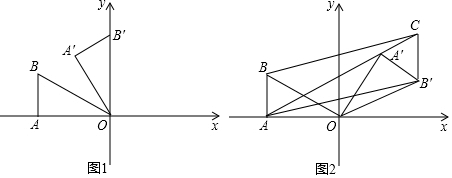
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
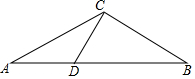 如图,在△ABC中,∠A=30°,D为边AB上的点,且DA=DC=2,若△DCB绕点D逆时针旋转,使DB、DC分别与线段AC相交于M、N,则当△DMN为等边三角形时,DM的长值为$\frac{2\sqrt{3}}{3}$.
如图,在△ABC中,∠A=30°,D为边AB上的点,且DA=DC=2,若△DCB绕点D逆时针旋转,使DB、DC分别与线段AC相交于M、N,则当△DMN为等边三角形时,DM的长值为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码/码 | 38 | 39 | 40 | 41 |
| 频数 | 5 | 15 | a | 10-a |
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com