解:(1)∵A(3,m),B(-2,n)在双曲线y=

上,
∴A(3,2),B(-2,-3),
∵直线y=kx经过C(-2,2),
∴y=-x,
(2)设AC与y轴相交于点D,则CD⊥OD,且CD=OD,
∴∠OCD=45°,同理∠BCO=45°,
∴∠ACO=∠BCO=45°,
∴∠ACP=∠BCP=135°,
又∵CP=CP,AC=BC=5,
∴△ACP≌△BCP(SAS);
(3)∵C
△APQ=PA+PQ+AQ=PB+PQ+AQ,
∴当B、P、Q三点在同一直线上时,△APQ的周长最小,
设直线PQ的解析式为y=kx+b,把B(-2,-3)、Q(0,6)代入,

,
∴y=

x+6,
联立方程

,
得

,
∴点P的坐标为(-
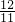
,
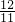
).
分析:(1)根据点A(3,m),B(-2,n)在反比例函数y=

的图象上即可求出点A、B的坐标,由直线y=kx经过C(-2,2),即可求出y=kx的解析式;
(2)设AC与y轴相交于点D,则CD⊥OD,且CD=OD,再证明∠ACP=∠BCP=135°,结合CP=CP,AC=BC=5即可求出两三角形全等;
(3)当B、P、Q三点在同一直线上时,△APQ的周长最小,设直线PQ的解析式为y=kx+b,把B(-2,-3)、Q(0,6)代入,求出解析式,联立两解析式,求出P点坐标.
点评:本题主要考查反比例函数的综合题,解答本题的关键是熟练掌握反比例函数的性质以及全等三角形性质等知识,此题难度不大,但是此类型的试题是中考的重点,希望同学们注意.

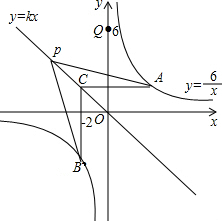 如图,点A(3,m),B(-2,n)在反比例函数y=
如图,点A(3,m),B(-2,n)在反比例函数y= 的图象上,直线y=kx经过点C(-2,2),点P是直线y=kx上任意一点.
的图象上,直线y=kx经过点C(-2,2),点P是直线y=kx上任意一点. 上,
上, ,
, x+6,
x+6, ,
, ,
,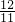 ,
,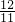 ).
). 的图象上即可求出点A、B的坐标,由直线y=kx经过C(-2,2),即可求出y=kx的解析式;
的图象上即可求出点A、B的坐标,由直线y=kx经过C(-2,2),即可求出y=kx的解析式;

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2