

���� ��1������������ȵ������������Ƽ��ɵó����ۣ�
��2�������$\frac{EC}{CG}$��$\frac{DF}{DG}$�������жϳ���ACE�ա�DBF���ɵó����ۣ�
Ӧ�ã������$\frac{{S}_{��BDH}}{{S}_{��ODH}}=\frac{1}{m+1}$�������ó�${S}_{��BDH}=1-\frac{1}{2}k$�����ɵó����ۣ�
��� �⣺��1���ߡ�ACE=��DCG����AEC=��DGC=90�㣬
���ACE�ס�DCG
��$\frac{EC}{CG}=\frac{AC}{CD}=\frac{1}{n}$��
��2����G��a��b��
��C��$\frac{k}{b}��b$�� D��a��$\frac{k}{a}$����
��EC=$\frac{k}{b}$��CG=a-$\frac{k}{b}$��DF=$\frac{k}{a}$��DG=b-$\frac{k}{a}$��
��$\frac{EC}{CG}=\frac{\frac{k}{b}}{a-\frac{k}{b}}=\frac{k}{ab-k}$��$\frac{DF}{GD}=\frac{\frac{k}{a}}{b-\frac{k}{a}}=\frac{k}{ab-k}$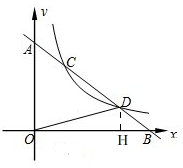
�ɣ�1��֪����ACE�ס�DCG��
��$\frac{EC}{CG}$=$\frac{k}{ab-k}$��
ͬ������DCG�ס�DBF��
��$\frac{DF}{DG}=\frac{k}{ab-k}$��
����ACE���DBF���͡�DCG���ƣ������Ʊȶ�Ϊ$\frac{k}{ab-k}$��
���ACE�ա�DBF
��AC=BD��
Ӧ�ã���ͼ������D��DH��x���ڵ�H
�ɣ�2���ɵ�AC=BD
��$\frac{BD}{CD}=\frac{1}{m}$��
��$\frac{BD}{AD}=\frac{1}{m+1}=\frac{BH}{OH}$��
��$\frac{{S}_{��BDH}}{{S}_{��ODH}}=\frac{1}{m+1}$��
�֡�${S}_{��OBD}=1��{S}_{��ODH}=\frac{1}{2}k$��
��${S}_{��BDH}=1-\frac{1}{2}k$��
��$\frac{1-\frac{1}{2}k}{\frac{1}{2}k}=\frac{1}{m+1}$��
��$k=\frac{2m+2}{m+2}$��
���� �����Ƿ����������ۺ��⣬��Ҫ���������������ε��ж������ʣ�ȫ�������ε��ж������ʣ��⣨2���Ĺؼ������$\frac{EC}{CG}$��$\frac{DF}{DG}$���⣨3���Ĺؼ��ǵó�������BDH���������һ�����͵���Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 1978�� | 1980�� | 1998�� |
| ������ũ���������Ԫ�� | 2000 | 0 | 2700 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
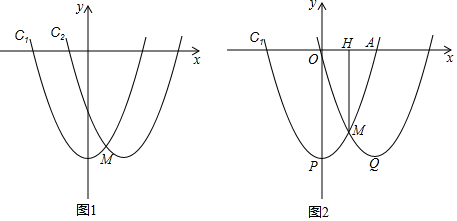
 ��ͼ���ڱ߳�Ϊ1����������������һֱ������ϵ�����У�A��Ϊ��-3��0����B��Ϊ��-1��2��
��ͼ���ڱ߳�Ϊ1����������������һֱ������ϵ�����У�A��Ϊ��-3��0����B��Ϊ��-1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
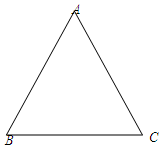 ��ͼ����֪�ڡ�ABC�У�AB=AC=10��tan��B=$\frac{4}{3}$��
��ͼ����֪�ڡ�ABC�У�AB=AC=10��tan��B=$\frac{4}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������OABC�У�OA=3��OC=5��OA��OC�ֱ���x�ᣬy���ϣ�D�DZ�CB�ϵ�һ�����㣨����C��B�غϣ�������������y=$\frac{k}{x}$��k��0����ͼ����D�����BA���ڵ�E������DE��
��ͼ������OABC�У�OA=3��OC=5��OA��OC�ֱ���x�ᣬy���ϣ�D�DZ�CB�ϵ�һ�����㣨����C��B�غϣ�������������y=$\frac{k}{x}$��k��0����ͼ����D�����BA���ڵ�E������DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
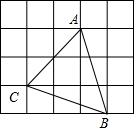 ��ͼ��������С�����εı߳���Ϊ1����A��B��C���ڸ���ϣ����ABC������ֵ�ǣ�������
��ͼ��������С�����εı߳���Ϊ1����A��B��C���ڸ���ϣ����ABC������ֵ�ǣ�������| A�� | $\frac{3}{5}$ | B�� | $\frac{2\sqrt{5}}{5}$ | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com