
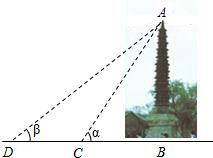
 为了测得聊城铁塔的高度,小明在离铁塔10米处的点C测得塔顶A的仰角为α,小亮在离铁塔25米处的点D测得塔顶A的仰角为β(如图),恰巧α+β=90度.小明和小亮很快求出了铁塔AB的高度.你知道他俩是怎样求出来的吗?请写出你的解题过程(结果精确到0.01米).
为了测得聊城铁塔的高度,小明在离铁塔10米处的点C测得塔顶A的仰角为α,小亮在离铁塔25米处的点D测得塔顶A的仰角为β(如图),恰巧α+β=90度.小明和小亮很快求出了铁塔AB的高度.你知道他俩是怎样求出来的吗?请写出你的解题过程(结果精确到0.01米).科目:初中数学 来源: 题型:
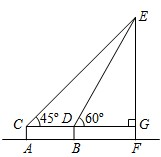 (2011•聊城)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑.铁塔由塔身和塔座两部分组成.为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°.已知测角仪AC的高为1.6m,CD的长为6m,CD所在的水平线CG⊥EF于点G.求铁塔EF的高(精确到0.1m).
(2011•聊城)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑.铁塔由塔身和塔座两部分组成.为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°.已知测角仪AC的高为1.6m,CD的长为6m,CD所在的水平线CG⊥EF于点G.求铁塔EF的高(精确到0.1m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com