����⣺��1�����ı���OABC�Ǿ��Σ�
���AOC=��OAB=90�㣬
��ODƽ�֡�AOC��
���AOD=��DOQ=45�㣬
����Rt��AOD�У���ADO=45�㣬
��AO=AD=2��OD=2
��
��t=
=2��
��2��Ҫʹ��PQBΪֱ�������Σ���Ȼֻ�С�PQB=90����PBQ=90�㣮
��ͼ1����PG��OC�ڵ�G����Rt��POG�У�
�ߡ�POQ=45�㣬���OPG=45�㣬
��OP=
t����OG=PG=t��
���P��t��t��
�֡�Q��2t��0����B��6��2����
���ݹ��ɶ����ɵã�PB
2=��6-t��
2+��2-t��
2��QB
2=��6-2t��
2+2
2��PQ
2=��2t-t��
2+t
2=2t
2��
������PQB=90�㣬����PQ
2+BQ
2=PB
2��
����2t
2+[��6-2t��
2+2
2]=��6-t��
2+��2-t��
2��
�����ã�4t
2-8t=0��
��ã�t
1=0����ȥ����t
2=2��
��t=2��
������PBQ=90�㣬����PB
2+QB
2=PQ
2��
��[��6-t��
2+��2-t��
2]+[��6-2t��
2+2
2]=2t
2��
�����ã�t
2-10t+20=0��
��ã�t=5��
��
�൱t=2��t=5+
��t=5-
ʱ����PQBΪֱ�������Σ�
�ⷨ2������ͼ2������PQB=90��ʱ��
��֪��OPQ=90�㣬��BQ��OD���BQC=��POQ=45��
�ɵ�QC=BC=2����OQ=4��
��2t=4��
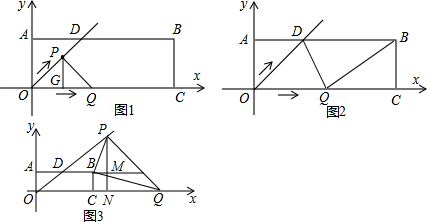
��t=2��
����ͼ3������PBQ=90��ʱ������Q��OC�ϣ�
��PN��x���ڵ�N����AB�ڵ�M��
����֤��PBM=��CBQ��
���PMB�ס�QCB
��
=
��
��CB•PM=QC•MB��
��2��t-2��=��2t-6����t-6����
�����t
2-10t+20=0��
��ã�t=5��
��
��t=5-
��
����ͼ3������PBQ=90��ʱ������Q��OC���ӳ����ϣ�
��PN��x���ڵ�N����AB�ӳ����ڵ�M��
����֤��BPM=��MBQ=��BQC��
���PMB�ס�QCB��
��
=
��
��CB•PM=QC•MB��
��2��t-2��=��2t-6����t-6����
�����t
2-10t+20=0��
��ã�t=5��
��
��t=5+
��
��3������������tֵ���������£�
����PQB��ij����ת180�㣬������Ӧ����ǡ�ö������������ϣ�
����ת����ΪPQ�е㣬��ʱ�ı���PBQB��Ϊƽ���ı��Σ�
��PO=PQ����P��t��t����Q��2t��0����֪��ת��������ɱ�ʾΪ��
t��
t����
�ߵ�B����Ϊ��6��2�������B�������Ϊ��3t-6��t-2����
����y=-
��x-t��
2+t���ã�2t
2-13t+18=0��
��ã�t
1=
��t
2=2��

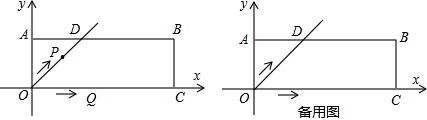




 ��2013•���ݣ���ͼ��������ABCD�У��߳�Ϊ10����A=60�㣮˳����������ABCD�����е㣬�ɵ��ı���A1B1C1D1��˳�������ı���A1B1C1D1�����е㣬�ɵ��ı���A2B2C2D2��˳�������ı�
��2013•���ݣ���ͼ��������ABCD�У��߳�Ϊ10����A=60�㣮˳����������ABCD�����е㣬�ɵ��ı���A1B1C1D1��˳�������ı���A1B1C1D1�����е㣬�ɵ��ı���A2B2C2D2��˳�������ı�
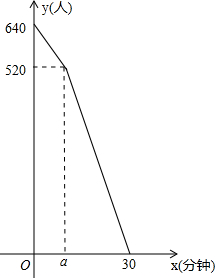 ��2013•���ݣ�����•һ�����ڣ�ij����վ�ÿ��������������ÿ�������Ҫ��ʱ���ŶӵȺ��Ʊ�������鷢�֣��ڳ�վ��ʼ��Ʊʱ����640���ŶӼ�Ʊ����Ʊ��ʼ�������ÿͼ���ǰ���ŶӼ�Ʊ��վ�����ÿͰ��̶����ٶ����ӣ���Ʊ�ڼ�Ʊ���ٶ�Ҳ�ǹ̶��ģ���Ʊʱ��ÿ���Ӻ��������ŶӼ�Ʊ��վ16�ˣ�ÿ����ÿ����Ʊ�ڼ�Ʊ14�ˣ���֪��Ʊ��ǰa����ֻ������������Ʊ�ڣ�ijһ������ŶӵȺ��Ʊ������y���ˣ����Ʊʱ��x�����ӣ��Ĺ�ϵ��ͼ��ʾ��
��2013•���ݣ�����•һ�����ڣ�ij����վ�ÿ��������������ÿ�������Ҫ��ʱ���ŶӵȺ��Ʊ�������鷢�֣��ڳ�վ��ʼ��Ʊʱ����640���ŶӼ�Ʊ����Ʊ��ʼ�������ÿͼ���ǰ���ŶӼ�Ʊ��վ�����ÿͰ��̶����ٶ����ӣ���Ʊ�ڼ�Ʊ���ٶ�Ҳ�ǹ̶��ģ���Ʊʱ��ÿ���Ӻ��������ŶӼ�Ʊ��վ16�ˣ�ÿ����ÿ����Ʊ�ڼ�Ʊ14�ˣ���֪��Ʊ��ǰa����ֻ������������Ʊ�ڣ�ijһ������ŶӵȺ��Ʊ������y���ˣ����Ʊʱ��x�����ӣ��Ĺ�ϵ��ͼ��ʾ��