解:(1)原式=3x-6y-3x+y
=-5y;
(2)(-2ab)(3a
2-2ab-b)
2=(-2ab)[(3a
2-2ab)-b]
2
=-2ab•(9a
4-12a
3b+4a
2b
2+b
2-6a
2b+4ab
2),
=-18a
5b+24a
4b
2-8a
3b
3-2ab
3+12a
3b
2-8a
2b
3(3)
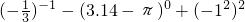
=-3-1+1
=-3;
(4)(a+b-3)(a+b+3)
=[(a+b)-3][(a+b)+3]
=(a+b)
2-9
=a
2+2ab+b
2-9;
(5)(x-1)(x+3)-(x-2)
2
=x
2+3x-x-3-(x
2-4x+4)
=x
2+2x-3-x
2+4x-4
=6x-7.
分析:(1)首先根据乘法分配原则进行乘法运算、再去括号,然后合并同类项即可;
(2)先利用完全平方公式把(3a
2-2ab-b)
2展开,再根据单项式乘以多项式的运算法则计算即可;
(3)利用负整数指数幂:a
-p=

(a≠0,p为正整数)和零指数幂:a
0=1(a≠0)运算即可;
(4)先分组再利用平方差公式和完全平方公式运算即可;
(5)利用多项式乘以多项式以及平方差公式运算即可.
点评:(1)本题考查了整式的混合运算,掌握其运算顺序和各种运算法则是解题的关键;
(2)本题考查了单项式乘以多项式的运算,在运算中注意乘法公式的运用;
(3)本题考查了负整数指数幂:a
-p=

(a≠0,p为正整数)和零指数幂:a
0=1(a≠0)的运算;
(4)本题考查了平方差公式和完全平方公式的运算,记熟公式是解题关键;
(5)本题考查了整式的混合运算,掌握其运算顺序和各种运算法则是解题的关键.

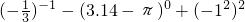
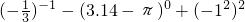
 (a≠0,p为正整数)和零指数幂:a0=1(a≠0)运算即可;
(a≠0,p为正整数)和零指数幂:a0=1(a≠0)运算即可; (a≠0,p为正整数)和零指数幂:a0=1(a≠0)的运算;
(a≠0,p为正整数)和零指数幂:a0=1(a≠0)的运算;

 导学全程练创优训练系列答案
导学全程练创优训练系列答案