
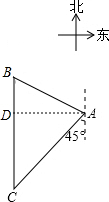
 如图,已知位于A处的中国渔政船在陆地指挥中心B的南偏东60°方向且相距
如图,已知位于A处的中国渔政船在陆地指挥中心B的南偏东60°方向且相距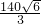 海里.某一刻接到陆地指挥中心的命令,一渔船有险情,需要救援.此时出事渔船在点C处,位于陆地指挥中心正南方向,位于渔政船西南方向.渔政船最大航速20海里/时.根据以上信息,请你求出渔政船赶往出事地点需要多少时间.
海里.某一刻接到陆地指挥中心的命令,一渔船有险情,需要救援.此时出事渔船在点C处,位于陆地指挥中心正南方向,位于渔政船西南方向.渔政船最大航速20海里/时.根据以上信息,请你求出渔政船赶往出事地点需要多少时间. 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
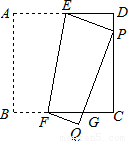
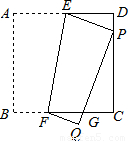
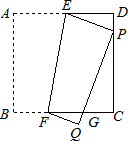 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.查看答案和解析>>
科目:初中数学 来源:第29章《相似形》中考题集(19):29.5 相似三角形的性质(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第4章《相似三角形》中考题集(19):4.3 两个三角形相似的判定(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年北京市顺义区中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com