
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,E是BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,E是BC的中点.| BC |
| AB |
| 4 |
| 5 |

| 1 |
| 2 |
| BC |
| AB |
| 4 |
| 5 |
| 1 |
| 2 |

| DE |
| DF |
| 4 |
| 5 |
| 5 |
| 4 |
| 5 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
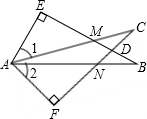 如图,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△AMB;④CD=DN.其中正确的结论是( )
如图,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△AMB;④CD=DN.其中正确的结论是( )| A、①②③ | B、①③④ |
| C、①② | D、②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据
如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com