
ШчЭМЂйЃЌжБНЧШ§НЧаЮAOBжаЃЌЁЯAOB=90ЁуЃЌABЦНаагкxжсЃЌOA=2OBЃЌAB=5ЃЌЗДБШР§КЏЪ§ ЕФЭМЯѓОЙ§ЕуAЃЎ
ЃЈ1ЃЉжБНгаДГіЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌPЃЈxЃЌyЃЉдкЃЈ1ЃЉжаЕФЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЦфжа1ЃМxЃМ8ЃЌСЌНгOPЃЌЙ§O зїOQЁЭOPЃЌЧвOP=2OQЃЌСЌНгPQЃЎЩшQзјБъЮЊЃЈmЃЌnЃЉЃЌЦфжаmЃМ0ЃЌnЃО0ЃЌЧѓnгыmЕФКЏЪ§НтЮіЪНЃЌВЂжБНгаДГіздБфСПmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєQзјБъЮЊЃЈmЃЌ1ЃЉЃЌЧѓЁїPOQЕФУцЛ§ЃЎ

НтЃКЃЈ1ЃЉШчЭМЂйЃЌЁпЁЯAOB=90ЁуЃЌ
ЁрOA2+OB2=AB2ЃЌ
ЁпOAOA=2OBЃЌAB=5ЃЌ
Ёр4OB2+OB2=25ЃЌНтЕУOB=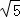 ЃЌ
ЃЌ
ЁрOA=2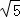 ЃЌ
ЃЌ
ЁпABABЦНаагкxжсЃЌ
ЁрOCЁЭABЃЌ
Ёр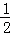 OC•AB=
OC•AB=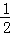 OB•OAЃЌМДOC=
OB•OAЃЌМДOC=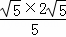 =2ЃЌ
=2ЃЌ
дкRtЁїAOCжаЃЌAC=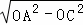 =4ЃЌ
=4ЃЌ
ЁрAЕузјБъЮЊЃЈ4ЃЌ2ЃЉЃЌ
ЩшЙ§AЕуЕФЗДБШР§КЏЪ§НтЮіЪНЮЊy=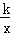 ЃЌ
ЃЌ
Ёрk=4ЁС2=8ЃЌ
ЁрЗДБШР§КЏЪ§НтЮіЪНЮЊy=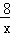 ЃЛ
ЃЛ
ЃЈ2ЃЉЗжБ№Й§PЁЂQзїxжсДЙЯпЃЌДЙзуЗжБ№ЮЊDЁЂHЃЌШчЭМЂкЃЌ
ЁпOQOQЁЭOPЃЌ
ЁрЁЯPOH+ЁЯQOD=90ЁуЃЌ
ЁпЁЯPOH+ЁЯOPH=90ЁуЃЌ
ЁрЁЯQOD=ЁЯOPHЃЌ
ЁрRtЁїPOHЁзRtЁїOQDЃЌ
Ёр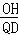 =
=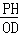 =
=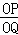 ЃЌ
ЃЌ
ЁпPPЃЈxЃЌyЃЉдкЃЈ1ЃЉжаЕФЗДБШР§КЏЪ§ЭМЯѓЩЯЃЌЦфжа1ЃМxЃМ8ЃЌQЕуЕузјБъЮЊЃЈmЃЌnЃЉЃЌЦфжаmЃМ0ЃЌnЃО0ЃЌOP=2OQЃЌ
ЁрPH=yЃЌOH=xЃЌOD=ЉmЃЌQD=nЃЌ
Ёр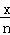 =
=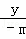 =2ЃЌНтЕУx=2nЃЌy=Љ2mЃЌ
=2ЃЌНтЕУx=2nЃЌy=Љ2mЃЌ
Ёпy=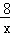 ЃЌ
ЃЌ
Ёр2n•ЃЈЉ2mЃЉ=8ЃЌ
Ёрmn=Љ2ЃЈЉ4ЃМmЃМЉ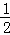 ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЁпn=1ЪБЃЌm=Љ2ЃЌМДQЕузјБъЮЊЃЈЉ2ЃЌ1ЃЉЃЌ
ЁрOQ=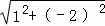 =
=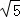 ЃЌ
ЃЌ
ЁрOP=2OQ=2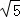 ЃЌ
ЃЌ
ЁрSЁїPOQ=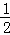 ЁС
ЁС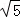 ЁС2
ЁС2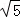 =5ЃЎ
=5ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШєЉ5x2ymгыxnyЪЧЭЌРрЯюЃЌдђm+nЕФжЕЮЊЃЈЁЁЁЁЃЉ
| ЁЁ | AЃЎ | 1 | BЃЎ | 2 | CЃЎ | 3 | DЃЎ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
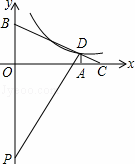
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїPBDЕФаББпPBТфдкyжсЩЯЃЌtanЁЯBPD=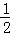 ЃЎбгГЄBDНЛxжсгкЕуCЃЌЙ§ЕуDзїDAЁЭxжсЃЌДЙзуЮЊAЃЌOA=4ЃЌOB=3ЃЎ
ЃЎбгГЄBDНЛxжсгкЕуCЃЌЙ§ЕуDзїDAЁЭxжсЃЌДЙзуЮЊAЃЌOA=4ЃЌOB=3ЃЎ
ЃЈ1ЃЉЧѓЕуCЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуDдкЗДБШР§КЏЪ§y=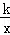 ЃЈkЃО0ЃЉЕФЭМЯѓЩЯЃЌЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈkЃО0ЃЉЕФЭМЯѓЩЯЃЌЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШчЭМЃЌжБЯпy=2x+4гыxЃЌyжсЗжБ№НЛгкAЃЌBСНЕуЃЌвдOBЮЊБпдкyжсгвВрзїЕШБпШ§НЧаЮOBCЃЌНЋЕуCЯђзѓЦНвЦЃЌЪЙЦфЖдгІЕуCЁфЧЁКУТфдкжБЯпABЩЯЃЌдђЕуCЁфЕФзјБъЮЊЁЁЁЁЃЎ
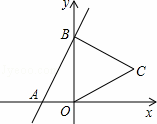
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЭМЂйЪЧЕчзгЦСФЛЕФОжВПЪОвтЭМЃЌ4ЁС4ЭјИёЕФУПИіаЁе§ЗНаЮБпГЄОљЮЊ1ЃЌУПИіаЁе§ЗНаЮЖЅЕуНазіИёЕуЃЌЕуAЃЌBЃЌCЃЌDдкИёЕуЩЯЃЌЙтЕуPДгADЕФжаЕуГіЗЂЃЌАДЭМЂкЕФГЬађвЦЖЏ
ЃЈ1ЃЉЧыдкЭМЂйжагУдВЙцЛГіЙтЕуPОЙ§ЕФТЗОЖЃЛ
ЃЈ2ЃЉдкЭМЂйжаЃЌЫљЛЭМаЮЪЧЁЁ ЁЁЭМаЮЃЈЬюЁАжсЖдГЦЁБЛђЁАжааФЖдГЦЁБЃЉЃЌЫљЛЭМаЮЕФжмГЄЪЧЁЁ ЁЁЃЈНсЙћБЃСєІаЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЙлВьЯТУцЭМАИЃЌдкAЃЌBЃЌCЃЌDЫФЗљЭМАИжаЃЌФмЭЈЙ§ЭМАИЃЈ1ЃЉЦНвЦЕУЕНЕФЪЧЃЈ ЃЉ
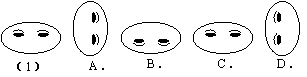 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ФГДЮЁАгАТдЫЁБжЊЪЖОКШќжаЙВга20ЕРЬтЃЌЖдгкУПвЛЕРЬтЃЌД№ЖдСЫ10ЗжЃЌД№ДэСЫЛђВЛ Д№Пл5ЗжЃЌжСЩйвЊД№ЖдЃЈЁЁЁЁЃЉЕРЬтЃЌЦфЕУЗжВХЛсВЛЩйгк95ЗжЃП
Д№Пл5ЗжЃЌжСЩйвЊД№ЖдЃЈЁЁЁЁЃЉЕРЬтЃЌЦфЕУЗжВХЛсВЛЩйгк95ЗжЃП
AЃЎ14ЁЁЁЁBЃЎ13ЁЁЁЁCЃЎ12ЁЁЁЁDЃЎ11
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ШчЭМЃЌОиаЮABCDжаЃЌвдЖдНЧЯпBDЮЊвЛБпЙЙГЩвЛИіОиаЮBDEFЃЌЪЙЕУСэвЛБпEFЙ§дОиаЮЕФЖЅЕуC
ЃЈ1ЃЉЩшRtЁїCBDЕФУцЛ§ЮЊS1ЃЌRtЁїBFCЕФУцЛ§ЮЊS2ЃЌRtЁїDCEЕФУцЛ§ЮЊS3ЃЌдђS1 S2+S3ЃЈгУЁАЃОЁБЁЂЁА=ЁБЁЂЁАЃМЁБЬюПеЃЉЃЛ
ЃЈ2ЃЉаДГіШчЭМжаЕФШ§ЖдЯрЫЦШ§НЧаЮЃЌВЂбЁдёЦфжавЛЖдНјаажЄУїЃЎ
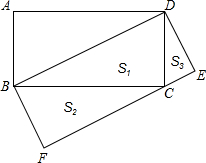
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com