
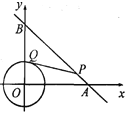
【题目】如图,⊙O是以原点为圆心,![]() 为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则
为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则![]() 的最小值为( )
的最小值为( )
A.3 B.4![]() C.6-
C.6-![]() D.2
D.2![]()
【答案】D
【解析】
试题分析:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键是确定OP垂直AB时S△PQO的值最小.先确定A点和B点坐标,再计算出AB=6![]() ,则OH=
,则OH=![]() AB=3
AB=3![]() ,再利用切线性质得到∠PQO=90°,根据勾股定理得到PQ=
,再利用切线性质得到∠PQO=90°,根据勾股定理得到PQ=![]() ,于是可判断OP最小时,PQ最小,S△PQO的值最小,然后求出此时PQ的长,再计算S△PQO的最小值.
,于是可判断OP最小时,PQ最小,S△PQO的值最小,然后求出此时PQ的长,再计算S△PQO的最小值.
解:作OH⊥AB于H,连接OQ、OP,如图,
当x=0时,y=-x+6=6,则B(0,6),
当y=0时,-x+6=0,解得x=6,则A(6,0),
∵OA=OB=6,
∴△OAB为等腰直角三角形,
∴AB=6![]() ,
,
∴OH=![]() AB=3
AB=3![]() ,
,
∵PQ为切线,
∴PQ⊥OQ,
∴∠PQO=90°,
∴PQ=![]() =
=![]() ,
,
∵PQ最小时,S△PQO的值最小,
∵OP最小时,PQ最小,
∴当OP⊥AB,即P点运动到H点时,OP最小,S△PQO的值最小,
此时PQ=![]() =4,
=4,
∴S△PQO的最小值=![]() ×
×![]() ×4=2
×4=2![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).


(1)b=______,点B的横坐标为_______(上述结果均用含c的代数式表示);
(2)连结BC,过点A作直线AE//BC,与抛物线交于点E.点D是x轴上一点,坐标为(2,0),当C、D、E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为正整数,则这样的△PBC共有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M,AD平分∠MAC,交BC于点D,AM交BE于点G.
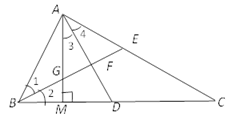
求证:(1) ∠BAM=∠C;
(2)判断直线BE与线段AD之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化校园环境,加大校园绿化投资.某区前年用于绿化的投资为18万元,今年用于绿化的投资为33万元,设这两年用于绿化投资的年平均增长率为x,则( )
A.18(1+2x)=33B.18(1+x2)=33
C.18(1+x)2=33D.18(1+x)+18(1+x)2=33
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com