
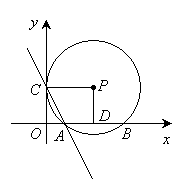
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系. 以点P为圆心, PC为半径的⊙P与x轴的正半轴交于A、B两点, 若抛物线y=ax2+bx+4经过A, B, C三点, 且AB=6.
⑴求⊙P的半径R的长;
⑵求该抛物线的解析式并直接写出该抛物线与⊙P的第四个交点E的坐标;
⑶若以AB为直径的圆与直线AC的交点为F, 求AF的长. (习题改编)
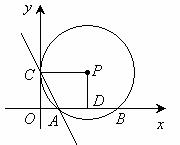
解:(1)连接AP
∵四边形ODPC为矩形
∴PD⊥AB
∴AD=BD=1/2AB=1/2×6=3 …………………………1分
又∵抛物线y=ax2+bx+4经过A, B, C三点
 ∴C(0,4) …………………………1分
∴C(0,4) …………………………1分
即OC=4
∴PD=OC=4
∴有勾股定理得AP=5 …………………………1分
∴⊙P的半径R的长为5
(2)∵OD=CP=AP=5
∴A(2,0) B(8,0)
求得函数解析式为 y=1/4(x-2)(x-8) …………………………2分
抛物线与⊙P的第四个交点E的坐标为(10,4)…………………………1分
(3)连接BF
∵AB为⊙D的直径
∴∠AFB=900=∠COA
又∵∠CAO=∠BAF
∴△AOC∽△AFB
∵AO=2 AC=![]() AB=6
AB=6
∴![]()
∴AF= ![]()


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
 PC为半径的⊙P与x轴的正半轴交于A、B两点,若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.
PC为半径的⊙P与x轴的正半轴交于A、B两点,若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.查看答案和解析>>
科目:初中数学 来源:月考题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》常考题集(26):6.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》常考题集(27):2.8 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com