
����Ŀ����ƽ���ĵ����ϣ������ɸ���ȫ��ͬ�ⳤ��С������ѳ�һ�������壬��ͼ��ʾ��
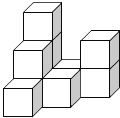
��1���뻭����������������ͼ��
��2����������������ı������ϻ�ɫ���ᣬ�������е�С�������У��� ��������ֻ��һ�����ǻ�ɫ���� ��������ֻ���������ǻ�ɫ���� ��������ֻ���������ǻ�ɫ��
��3������������ͷ����һЩ��ͬ��С�����壬������ָ���ͼ������ͼ���䣬�����������Ӽ���С�����壿
���𰸡���1��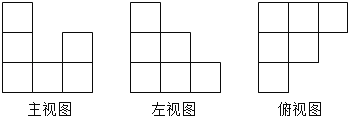 ��2��1����2����3������3��4��
��2��1����2����3������3��4��
��������
�����������1������֪������֪������ͼ��3�У�ÿ��С����������Ŀ�ֱ�Ϊ3��1��2������ͼ��3�У�ÿ��С��������Ŀ�ֱ�Ϊ3��2��1������ͼ��3�У�ÿ��С����������Ŀ�ֱ�Ϊ3��2��1���ݴ˿ɻ���ͼ�Σ�
��2��ֻ��һ�����ǻ�ɫ��Ӧ���ǵ�һ������������ײ��м��Ǹ�����2�����ǻ�ɫ��Ӧ�ǵ�һ����ײ�������Ǹ��͵ڶ���������Ǹ���ֻ���������ǻ�ɫ��Ӧ�ǵ�һ�еڶ����������Ǹ����ڶ�����ǰ���Ǹ�����������ײ��Ǹ���
��3�����ָ���ͼ������ͼ���䣬�����ڶ���ǰ��ļ������Ϸ�һ��С�����壬����ļ������Ϸ�3��С�����壮
�⣺��1����ͼ��ʾ��

��2��ֻ��һ�����ǻ�ɫ��Ӧ���ǵ�һ������������ײ��м��Ǹ�����1������2�����ǻ�ɫ��Ӧ�ǵ�һ����ײ�������Ǹ��͵ڶ���������Ǹ�����2����ֻ���������ǻ�ɫ��Ӧ�ǵ�һ�еڶ����������Ǹ����ڶ�����ǰ���Ǹ�����������ײ��Ǹ�����3����
��3��������������4��С�����壮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
![]()
��1��OA= cm��OB= cm��
��2������C���߶�AO��һ�㣬������AC=CO+CB����CO�ij���
��3��������P��Q�ֱ��A��Bͬʱ�����������˶�����P���ٶ�Ϊ2cm/s����Q���ٶ�Ϊ1cm/s�����˶�ʱ��Ϊt��s��������P���Q�غ�ʱ��P��Q����ֹͣ�˶���
����tΪ��ֵʱ��2OP��OQ=8��
������P������Oʱ������M�ӵ�O��������3cm/s���ٶ�Ҳ�����˶�������M�ϵ�Q���������أ���ͬ�����ٶ����P�˶���������P���������أ�����ͬ�����ٶ����Q�˶������������ֱ����P��Qֹͣʱ����MҲֹͣ�˶����ڴ˹����У���M��ʻ����·��Ϊ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���C=90������B=30����OΪAB���е㣬����ABC�Ƶ�O��ʱ����ת60������EDAλ�ã�����CD��
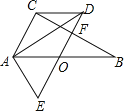
��1����֤��OD��BC��
��2����֤���ı���AODCΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ABC=90��������ֱ�ߺ�Բ�棬����Ҫ����ͼ����д������������ͼ�ۼ������������������⣮
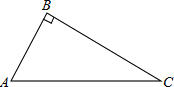
��1����AC�Ĵ�ֱƽ���ߣ��ֱ�AC��BC�ڵ�D��E��
��2����AB=12��BE=5������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ų�����ֽƬ������һ�������Σ�ʣ��һ�������Σ���Ϊ��һ�β�������ʣ�µij�����ֽƬ���ټ���һ�������Σ�ʣ��һ�������Σ���Ϊ�ڶ��β������������ڵ�n�β�����ʣ�µij�����Ϊ�����Σ����ԭ������Ϊn�����쳤���Σ���ͼ1��������ABCD�У���AB=2��BC=6����Ƴ�����ABCDΪ2�����쳤���Σ�
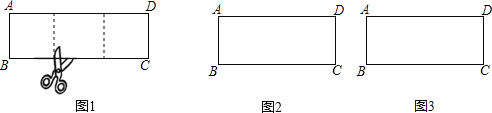
��1����������
��ͼ2��������ABCD��Ϊ10����Ϊ4���������쳤���Σ���д������ �����쳤���Σ�����ͼ�л����ü��ߣ�
��2��̽������㣺
��֪������ABCD��һ�߳�Ϊ30����һ�߳�Ϊa ��a��30����������3�����쳤���Σ��뻭�����п��ܵij�����ABCD���ü��ߵ�ʾ��ͼ���������Ӧ��aֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���ѧ����ȡ��Ѷ����Ҫ���������á�A���ֻ���B�����ӣ�C�����磬D�����ߵ��ˣ�E�����������ѡ������б�ѡ��ֻ��ѡһ��ĵ����ʾ����������ȡ50����ѧ�����и��ʾ����飬��õ���ķ�ʽ��_______�������ղ��������飩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����һ��O����A��Bͬʱ��O��������ֱ��l�Ϸֱ����������������˶�����A��B���ٶȱ�Ϊ1��2�����˶�ʱ��Ϊts��

��1����t=2sʱ��AB=12cm����ʱ��
����ֱ��l�ϻ���A��B�����˶�2��ʱ��λ�ã����ش��A�˶����ٶ��� cm/s�� ��B�˶����ٶ��� cm/s��
������PΪֱ��l��һ�㣬��PA��PB=OP����![]() ��ֵ��
��ֵ��
��2���ڣ�1���������£���A��Bͬʱ��ԭ�������˶����پ������룬OA=2OB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ACB=90����AC=CB��F��AB���ϵ��е㣬��D��E�ֱ���AC��BC�����˶�����ʼ�ձ���AD=CE������DE��DF��EF��
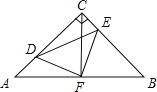
��1����֤����ADF�ա�CEF��
��2����֤����DFE�ǵ���ֱ�������Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com