
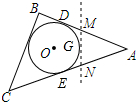
 如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.
如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是12cm.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.
如图,将3枚相同的硬币放入一个3×4的长方形格子中(每个小正方形格子只能放1枚硬币).则所放的3枚硬币中,任意两枚都不同行且不同列的概率为$\frac{6}{55}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com