
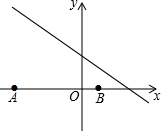
 如图,已知点A(-8,0),B(2,0),点C在直线y=-$\frac{3}{4}x+4$上,则使△ABC是直角三角形的点C的个数为( )
如图,已知点A(-8,0),B(2,0),点C在直线y=-$\frac{3}{4}x+4$上,则使△ABC是直角三角形的点C的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据∠A为直角,∠B为直角与∠C为直角三种情况进行分析.
解答 解:如图,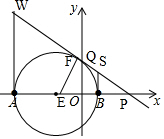
①当∠A为直角时,过点A作垂线与直线的交点W(-8,10),
②当∠B为直角时,过点B作垂线与直线的交点S(2,2.5),
③若∠C为直角
则点C在以线段AB为直径、AB中点E(-3,0)为圆心、5为半径的圆与直线y=-$\frac{3}{4}x+4$的交点上.
在直线y=-$\frac{3}{4}x+4$中,当x=0时y=4,即Q(0,4),
当y=0时x=$\frac{16}{3}$,即点P($\frac{16}{3}$,0),
则PQ=$\sqrt{{4}^{2}+(\frac{16}{3})^{2}}$=$\frac{20}{3}$,
过AB中点E(-3,0),作EF⊥直线l于点F,
则∠EFP=∠QOP=90°,
∵∠EPF=∠QPO,
∴△EFP∽△QOP,
∴$\frac{EF}{QO}$=$\frac{PE}{PQ}$,即$\frac{EF}{4}$=$\frac{3+\frac{16}{3}}{\frac{20}{3}}$,
解得:EF=5,
∴以线段AB为直径、E(-3,0)为圆心的圆与直线y=-$\frac{3}{4}x+4$恰好有一个交点.
所以直线y=-$\frac{3}{4}x+4$上有一点C满足∠C=90°.
综上所述,使△ABC是直角三角形的点C的个数为3,
故选:C.
点评 本题考查的是一次函数综合题,在解答此题时要分三种情况进行讨论,关键是根据圆周角定理判断∠C为直角的情况是否存在.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.1×103 | B. | 1.1×104 | C. | 1.1×105 | D. | 1.1×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com