
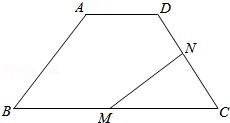
 如图,在梯形ABCD中,AD∥BC,AD=3,CD=5,BC=10,梯形的高为4,动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动;动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒
如图,在梯形ABCD中,AD∥BC,AD=3,CD=5,BC=10,梯形的高为4,动点M从点B出发沿线段BC以每秒2个单位长度向终点C运动;动点N同时从点C出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒分析 (1)直接利用梯形中位线的定理求出即可;
(2)平移梯形的一腰,根据平行四边形的性质和相似三角形的性质求解;
(3)利用MC=MN时,结合路程=速度×时间求得其中的有关的边,运用等腰三角形的性质和解直角三角形的知识求解.
解答 解:(1)∵AD=3,BC=10,
∴梯形ABCD的中位线长为:(3+10)÷2=6.5;
(2)如图1,过D作DG∥AB交BC于G点,则四边形ADGB是平行四边形.
∵MN∥AB,
∴MN∥DG,
∴BG=AD=3.
∴GC=10-3=7.
由题意知,当M、N运动到t秒时,CN=t,CM=10-2t.
∵DG∥MN,
∴△MNC∽△GDC.
∴$\frac{CN}{CD}$=$\frac{CM}{CG}$,
即$\frac{t}{5}$=$\frac{10-2t}{7}$.
解得,t=$\frac{50}{17}$;
(3)当MC=MN时,如图2,过M作MF⊥CN于F点,FC=$\frac{1}{2}$NC=$\frac{1}{2}$t.
∵∠C=∠C,∠MFC=∠DHC=90°,
∴△MFC∽△DHC,
∴$\frac{FC}{HC}$=$\frac{MC}{DC}$,
即$\frac{\frac{1}{2}t}{3}$=$\frac{10-2t}{5}$,
解得:t=$\frac{60}{17}$.
综上所述,t=$\frac{60}{17}$时,MC=MN.
点评 此题主要考查了四边形综合应用以及相似三角形的判定与性质和锐角三角函数等知识,注意梯形中常见的辅助线:平移一腰、作两条高.此题的知识综合性较强,能够从中发现平行四边形、等腰三角形等,根据它们的性质求解.


科目:初中数学 来源: 题型:解答题
 如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.
如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
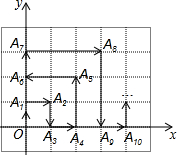 如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).
如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 168(1+x)2=108 | B. | 168(1-x)2=108 | C. | 168(1-2x)=108 | D. | 168y=x2(1-x2)=108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com