

解:(1)证明:
①∵四边形ABCD是矩形,
∴AD//BC.
∴∠CAD=∠ACB, ∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE全等△COF,
∴OE= OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形.
②设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得:42+ (8-x)2 =x2,
解得:x=5
∴ AF=5 cm-
(2)①显然当P点在AF上时,Q点在CD上
此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形。
∴以 A、C、P、Q四点为顶点的四边形是平行四边形时.PC=QA.
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t 秒,
∴PC=5t ,QA= 12-4t.
∴5t= 12-4t,
解得: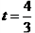
∴以 A、C、P、Q四点为顶点的四边形是平行四边形时
②由题意得,以 A、C、P、Q 四点为顶点的四边形是平行四边形时,点 P、Q在互相平行的对应边上,分三种情况:
i)如图1,当P点在AF 上、Q点在CE上时.AP= CQ,即a= 12 - b ,得a + b= 12.
ii)如图2,当P点在BF 上、Q点在DE上时.AQ= CP,即12 - b= a , 得a+ b= 12.
iii)如图3,当P点在AB 上、Q点在CD上时.AP= CQ,即12-a--=b,得 a+b=12.
综上所述,a 与b 满足的数量关系式是a十b=12(ab≠0). 


科目:初中数学 来源: 题型:
 已知:矩形ABCD,对角线AC、BD相交于点O.
已知:矩形ABCD,对角线AC、BD相交于点O.| BC |
| CD |
| AO |
| AD |
| AB |
| BC |
| BO |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).| MN | DN |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 | 7 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com