如图.将一根25cm长的细木棒放入长.宽.高的平方分别为64cm2.36cm2和300cm2的长方体无盖盒子中.则细木棒露在盒外面的最短长度是5cm．题目和参考答案——青夏教育精英家教网—

15．

如图，将一根25cm长的细木棒放入长、宽、高的平方分别为64cm²、36cm²和300cm²的长方体无盖盒子中，则细木棒露在盒外面的最短长度是5cm．

分析长方体内体对角线是最长的，当木条在盒子里对角放置的时候露在外面的长度最小，这样就是求出盒子的对角线长度即可．

解答解：由题意知：盒子底面对角线长的平方为：64+36=100，
盒子的对角线长：$\sqrt{100+300}$=20（cm），
细木棒长25cm，
故细木棒露在盒外面的最短长度是：25-20=5（cm）．
所以细木棒露在外面的最短长度是5厘米．
故答案为：5．

点评此题主要考查了勾股定理的应用，解题的关键是熟悉勾股定理并两次应用勾股定理．

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

练习册湖北教育出版社系列答案

新课标同步练习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

5．

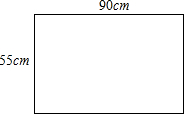现有一块长为90cm，宽为55cm的木板，能否采用如图的方式，在这块木板上截出两块面积分别是1200平方厘米和2700平方厘米的正方形木板？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．设一个三角形的三边长分别为a、b、c，P=$\frac{1}{2}$（a+b+c），则有下列面积公式：
S=$\sqrt{P（P-a）（P-b）（P-c）}$（海伦公式）；
S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-（\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}）^{2}]}$（秦九韶公式）．
（1）一个三角形边长依次为5、6、7，利用两个公式分别求这个三角形的面积；
（2）一个三角形边长依次为$\sqrt{5}$、$\sqrt{6}$、$\sqrt{7}$，利用两个公式分别求这个三角形的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．