
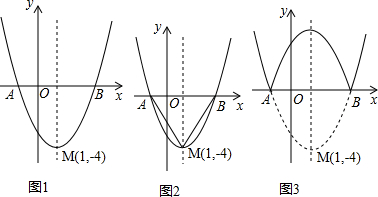
ЗжЮі ЃЈ1ЃЉгЩЖЅЕузјБъШЗЖЈmЁЂkЕФжЕЃЌдйСюy=0ЧѓЕУЭМЯѓгыxжсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉЩшДцдкетбљЕФPЕуЃЌгЩгкЕзБпЯрЭЌЃЌЧѓГіЁїPABЕФИп|y|ЃЌНЋyЧѓГіДњШыЖўДЮКЏЪ§БэДяЪНЧѓЕУPЕузјБъЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌВЛЗСЩшCЕуЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЕуEдкХзЮяЯпy=x2-2x-3ЩЯЃЎЕБBCЮЊе§ЗНаЮBCDEЕФБпЪБЃЌдђEЕуЕФзјБъЮЊЃЈmЃЌm2-2m-3ЃЉЃЌИљОне§ЗНаЮЕФБпГЄЯрЕШЃЌBC=DEСаГіЙигкmЕФЗНГЬЃЌЧѓНтМДПЩЃЎ
ЃЈ4ЃЉЛГіЗзЊКѓаТЕФКЏЪ§ЭМЯѓЃЌгЩжБЯпy=x+bШЗЖЈГіжБЯпвЦЖЏЕФЗЖЮЇЃЌЧѓГіbЕФШЁжЕЗЖЮЇЃЎ
НтД№ НтЃКЃЈ1ЃЉЁпMЃЈ1ЃЌ-4ЃЉЪЧЖўДЮКЏЪ§y=ЃЈx+mЃЉ2+kЕФЖЅЕузјБъЃЌ
Ёрy=ЃЈx-1ЃЉ2-4=x2-2x-3ЃЌ
ЕБx2-2x-3=0ЃЌНтЕУx1=-1ЃЌx2=3ЃЎ
ЁрAЁЂBСНЕуЕФзјБъЗжБ№ЮЊAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯДцдкЕуPЃЌЪЙSЁїPAB=$\frac{1}{4}$SMAB
ЩшPЃЈxЃЌyЃЉЃЌдђSЁїPAB=$\frac{1}{2}$|AB||y|ЃЌгжSЁїMAB=$\frac{1}{2}$|AB|ЁС|-4|=8ЃЌ
Ёр2|y|=$\frac{1}{4}$ЁС8ЃЌМДy=ЁР1ЃЌ
ЁпЖўДЮКЏЪ§ЕФзюаЁжЕЮЊ-4ЃЌ
Ёрy=ЁР1ЃЎ
ЕБy=1ЪБЃЌx=1+$\sqrt{5}$Лђx=1-$\sqrt{5}$ЃЎ
ЁрPЕузјБъЮЊЃЈ1+$\sqrt{5}$ЃЌ1ЃЉЛђЃЈ1-$\sqrt{5}$ЃЌ1ЃЉЃЛ
ЕБy=-1ЪБЃЌx=1+$\sqrt{3}$ЃЌx=1-$\sqrt{3}$ЃЌ
PЕузјБъЮЊЃЈ1+$\sqrt{3}$ЃЌ-1ЃЉЛђЃЈ1-$\sqrt{3}$ЃЌ-1ЃЉЃЛ
злЩЯЫљЪіЃКPЕузјБъЮЊЃЈ1+$\sqrt{5}$ЃЌ1ЃЉЃЌЃЈ1-$\sqrt{5}$ЃЌ1ЃЉЃЌЃЈ1+$\sqrt{3}$ЃЌ-1ЃЉЃЌЃЈ1-$\sqrt{3}$ЃЌ-1ЃЉЃЛ
ЃЈ3ЃЉВЛЗСЩшЕуEдкХзЮяЯпy=x2-2x-3ЩЯЃЌCЕуЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЎ
ЕБBCЮЊе§ЗНаЮBCDEЕФБпЪБЃЌдђEЕуЕФзјБъЮЊЃЈmЃЌm2-2m-3ЃЉЃЎ
ЁпЫФБпаЮBCDEЪЧе§ЗНаЮЃЌ
ЁрBC=DEЃЌ
Ёр|m-3|=|m2-2m-3|ЃЌ
МДm-3=m2-2m-3ЃЌЛђm-3=-ЃЈm2-2m-3ЃЉЃЌ
НтЕУm1=0ЃЌm2=3ЃЌЛђm1=-2ЃЌm2=3ЃЌ
ЕБm=3ЪБЃЌCЕугыBЕужиКЯЃЌВЛКЯЬтвтЃЌЩсШЅЃЌ
ЁрEЕуЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЛђЃЈ-2ЃЌ0ЃЉЃЌдђB1ЃЈ3ЃЌ4ЃЉЃЌB2ЃЈ3ЃЌ-4ЃЉЃЌ
ЃЈ4ЃЉШчЭМ3 ЃЌ
ЃЌ
вРЬтвтжЊЃЌЕБ-1ЁмxЁм3ЪБЃЌЗелКѓЕФХзЮяЯпЕФНтЮіЪНЮЊЃКy=-x2+2x+3
гыжБЯпy=x+bгыаТХзЮяЯпга1ИіНЛЕуЪБЃЌ-x2+2x+3=x+bЃЌМДx2-x-3-b=0ЃЌ
дђЁї=ЃЈ-1ЃЉ2-4ЁСЃЈ-3-bЃЉ=0ЃЌ
НтЕУ b=$\frac{13}{4}$
ЕБжБЯпy=x+bОЙ§AЃЈ-1ЃЌ0ЃЉЪБ-1+b=0ЃЌ
ПЩЕУb=1ЃЌ
гЩЬтвтПЩжЊy=x+bдкy=x+1ЕФЯТЗНЃЎ
гЩЭМПЩжЊЗћКЯЬтвтЕФbЕФШЁжЕЗЖЮЇ1ЁмbЁм$\frac{13}{4}$ЃЎ
ЙЪД№АИЪЧЃК1ЁмbЁм$\frac{13}{4}$ЃЎ
ЕуЦР БОЬтПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЌжаЕузјБъЙЋЪНЃЌСНЕуМфЕФОрРыЙЋЪНЃЌе§ЗНаЮЕФаджЪЃЌзлКЯадНЯЧПЃЌФбЖШНЯДѓЃЌЦфжаЃЈ3ЃЉНјааЗжРрЬжТлЪЧНтЬтЕФЙиМќЃЎ


 ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
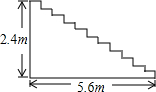 ФГБіЙндкжиаТзАаоКѓЃЌзМБИдкДѓЬќжїТЅЬнЩЯЦЬЩшФГжжКьЩЋЕиЬКЃЌвбжЊетжжЕиЬКУПЦНЗНУзЪлМл40дЊЃЌжїТЅЬнЕРПэ2УзЃЌЦфВрУцШчЭМЫљЪОЃЌдђЙКТђЕиЬКжСЩйашвЊ640дЊЃЎ
ФГБіЙндкжиаТзАаоКѓЃЌзМБИдкДѓЬќжїТЅЬнЩЯЦЬЩшФГжжКьЩЋЕиЬКЃЌвбжЊетжжЕиЬКУПЦНЗНУзЪлМл40дЊЃЌжїТЅЬнЕРПэ2УзЃЌЦфВрУцШчЭМЫљЪОЃЌдђЙКТђЕиЬКжСЩйашвЊ640дЊЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 0.129ЁС105 | BЃЎ | 1.29ЁС104 | CЃЎ | 12.9ЁС103 | DЃЎ | 129ЁС102 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com