
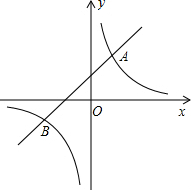
 如图,已知一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,已知一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.分析 (1)把点A坐标代入反比例函数求出m的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出n的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)找出直线在反比例函数图形的上方的自变量x的取值即可.
解答 解:(1)∵点A(2,4)在反比例函数y2=$\frac{m}{x}$的图象上,
∴m=2×4=8,
∴反比例函数的表达式为y2=$\frac{8}{x}$,
∵点B(-4,n)也在反比例函数y2=$\frac{8}{x}$的图象上,
∴n=$\frac{8}{-4}$=-2,
即B(-4,-2),
把点A(2,4),点B(-4,-2)代入一次函数y1=kx+b中,
得$\left\{\begin{array}{l}{2k+b=4}\\{-4k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴一次函数的表达式为y1=x+2;
故一次函数得到解析式为y1=x+2,反比例函数解析式为y2=$\frac{8}{x}$;
(2)当-4<x<0或x>2时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,此类题目的求解一般都是先把已知点的坐标代入反比例函数表达式求出反比例函数解析式,然后再求一次函数解析式,难度中等.


科目:初中数学 来源: 题型:解答题
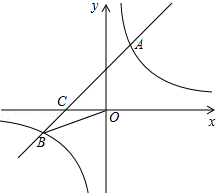 已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),BD⊥x轴,垂足为点D,且BD:OD=2:5,
已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),BD⊥x轴,垂足为点D,且BD:OD=2:5,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
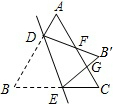 如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=95°,则∠EGC的度数为95°.
如图,等边三角形ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=95°,则∠EGC的度数为95°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 任意打开七年级下册数学教科书,正好是97页是确定事件 | |
| D. | 在相同条件下,只要试验的次数足够多,频率就可以作为概率的估计值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com