
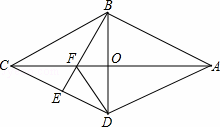
如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2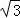 ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
(1)证明:在△ABC和△ADC中,
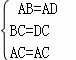 ,
,
∴△ABC≌△ADC(SSS),
∴∠BCA=∠DCA,
在△CBF和CADF中,
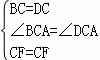 ,
,
∴△CBF≌△CDF(SAS),
(2)解:∵△ABC≌△ADC,
∴△ABC和△ADC是轴对称图形,
∴OB=OD,BD⊥AC,
∵OA=OC,
∴四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AC=2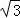 ,BD=2,
,BD=2,
∴OA=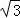 ,OB=1,
,OB=1,
∴AB=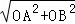 =
=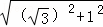 =2,
=2,
∴四边形ABCD的周长=4AB=4×2=8.
(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,∠BCD=∠BAD,
∵△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD+∠CBF=90°,∠EFD+∠CDF=90°,
∴∠EFD=∠BCD.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
在棋盘中建立如图所示的直角坐标系,三颗棋子A,O,B的位置如图,它们的坐标分别是(-1,1),(0,0)和(1,0).
(1)如图2,添加棋子C,使A,O,B, C四颗棋子成为一个轴对称图形,请在图 中画出该图形的对称轴.
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
利用对称变换可设计出美丽图案,如图,在方格纸中有一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出四边形关于直线l成轴对称的图形,再将你所作的图形和原四边形绕0点按顺时针旋转90°;
(2)完成上述图案设计后,可知这个图案的面积等于 20 .

查看答案和解析>>
科目:初中数学 来源: 题型:
下列运算正确的是( )
|
| A. | a2+a3=a5 | B. | (﹣2a2)3=﹣6a6 | C. | (2a+1)(2a﹣1)=2a2﹣1 | D. | (2a3﹣a2)÷a2=2a﹣1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,将一个边长为a的 正方形纸片剪去两个小矩形,得到一个“
正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )

|
| A. | 2a﹣3b | B. | 4a﹣8b | C. | 2a﹣4b | D. | 4a﹣10b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com